|
|
|
\require{AMSmath}



De maximale winst bepalen
Voor school moeten wij een probleem oplossen waarbij we de maximale winst moeten vinden, uitgetekend in een grafiek. Nu is het 6 jaar geleden dat ik voor het laatst economie en wiskunde heb gehad, en het oefenen met 2 andere opgaven was blijkbaar niet genoeg om ook deze opgave te begrijpen. Helaas lukte het me ook niet met de talloze voorbeelden op deze website....
Dit is de opgave:
Er zijn produkt A en B, en machine 1 en 2. Beide machines mogen maximaal 150 uur draaien. (M1$<$150, M2$<$150)
Produkt A heeft nodig: 2 uur machine1 + 4 uur machine2.
produkt B heeft nodig: 3 uur machine1 + 2 uur machine2.
Verkoopprijs prod.A = 300 euro, prod.kosten 100 euro (opbrengst is dan 200euro),
Verkoopprijs prod.B = 200 euro, prod.kosten 75 euro (opbrengst is dan 125 euro).
6000 Euro van het maximale overschot is te beschouwen als constante kosten.
Het lukt me om enkele vergelijkingen te maken, maar het wordt een chaos wanneer ik alles in een grafiek probeer te zetten of probeer uit te rekenen.... maar zo moeilijk kan het toch niet zijn?! Ik geloof dat de produkten A en B als x en y tegenover elkaar in een grafiek worden uitgezet, maar welke vergelijkingen nog meer? Kortom: chaos! :)
Alvast hartelijke dank!
anke
Student hbo - maandag 7 maart 2005
Antwoord
Noem het aantal producten A maar a en het aantal producten B maar b. Probeer de andere 'zaken' dan uit te drukken in a en b.
Voor a producten A en b producten B dan heeft M1 toch 2a+3b uren nodig. Maar 2a+3b moet wel kleiner dan 150 zijn. Zoiets kan je ook doen voor machine M2. Totale tijd is 4a+2b en dat moet ook kleiner dan 150 zijn.
2a+3b$<$150
4a+2b$<$150
Deze twee vergelijking geven een gebied aan waarbinnen a en b moeten liggen. Laten we dat maar eens tekenen!
Teken de grafieken van 2a+3b=150 en 4a+2b=150. Dit doe je handig met a=0, wat is b? en b=0 wat is a? Je krijgt dan uiteindelijk een grafiek met een toegestaan gebied (a horizontaal en b verticaal)
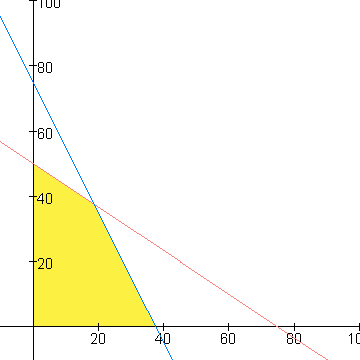
Dan maak je een doelfunctie waarbij je de winst uitdrukt in a en b. Afhankelijk van de 'richting' van deze doelfunctie bepaal je in welk 'punt' de winst maximaal is door verschillende niveaulijnen te tekenen.
Winst=200·a+125·b-6000
Teken bijvoorbeeld eens de grafiek als de winst 500 of 4000 is... Je krijgt dan:
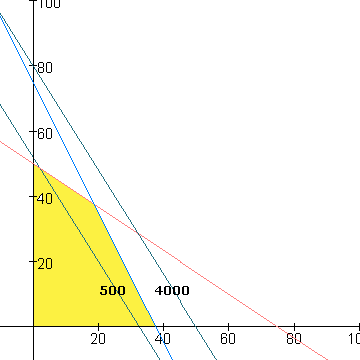
Kortom: de maximale winst zal wel in het snijpunt van de twee grafieken liggen, dus:
2a+3b=150
4a+2b=150
4a+6b=300
4a+2b=150
--------- -
4b=150
b=37,5
a=18,25
Nu is dat een beetje lastig... Dus moet je even rondom dat punt kijken welke gehele waarden van a en b nu 'echt' de meeste winst geven. Hopelijk helpt dat een beetje...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 maart 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











