WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cartesische vergelijkingen

Bewijs dat in een geijkte ruimte het vlak door P1(x1,y1,z1),P2(x2,y2,z2) en evenwijdig met een rechte met stel richtingsgetallen (a,b,c) de volgende vergelijking heeft:
x  y  z  1
x1 y1 z1 1
x2 y2 z2 1
a  b  c  0
(Wat ik hierboven heb geschreven is een determinant die gelijk moet zijn aan 0)
ik ben hier echt niet goed in
giovan
3de graad ASO - dinsdag 1 maart 2005

Antwoord

dag Giovanni,

We zoeken een vergelijking van een vlak, ofwel een lineair verband tussen x, y en z.

Ik hoop dat duidelijk is dat deze determinant in ieder geval een lineair verband aangeeft tussen x, y en z.

Als we nu kunnen aantonen dat de punten P1 en P2 voldoen aan deze vergelijking, dan zijn we al een heel eind.

Een determinant is gelijk aan 0 als er een afhankelijkheid is van de rijen (of de kolommen).

Vul nu voor x, y en z de coördinaten van P1 in. Dan zijn de eerste en de tweede rij gelijk, dus is de determinant gelijk aan 0.

Iets dergelijks voor P2.

Ingewikkelder wordt het met die eis van de evenwijdige rechte.

Ik ben er niet zeker van of er een slimmere methode is, maar je kunt in ieder geval de volgende manier uitvoeren, met ijverig handwerk.

Er moet gelden dat de richtingsvector van de genoemde rechte loodrecht staat op de normaalvector van deze vergelijking.
Je kunt de determinant ontwikkelen naar de eerste rij, waardoor de normaalvector direct zichtbaar wordt (genoteerd met onderdeterminanten):

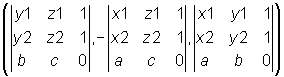
Nu het inproduct nemen van de vector (a, b, c) met deze normaalvector, en jawel: alles valt tegen elkaar weg en het resultaat is 0.

Conclusie: de genoemde determinant is inderdaad de gezochte vergelijking.
Groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 maart 2005

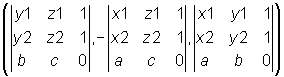
Re: Cartesische vergelijkingen