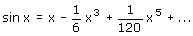|
|
|
\require{AMSmath}
Reeks van Euler
Geachte mijnheer of mevrouw,
Er is een wiskundig probleem waar ik helaas niet uit kan komen. De vraag luidt als volgt:
Bewijs
 2/6 = 1/1 + 1/4 + 1/9 + 1/16 + 1/25........ .
Ik heb geprobeerd om deze reeks d.m.v. volledige inductie en bewijs uit het ongerijmde aan te tonen maar het is me niet gelukt.
Ik hoop u hiermede voldoende te hebben geinformeerd.
Hoogachtend,
Ahmet Ayyildiz
Ahmet
Student universiteit - donderdag 30 mei 2002
Antwoord
In de Pythagoras van april 2002 staat een uitvoerig bewijs van deze 'som'. Het begint met de formule van Newton:
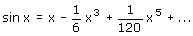
Door links en recht te delen door 'x' en daarna 'x' te vervangen door 'px' krijg je 'iets' wat later mooier uitkomt. Dit bewijs bestrijkt nog een pagina, zodat ik zou zeggen, dat je het beste even kan kijken in het betreffende nummer. In de mediatheek hebben ze het vast en anders in elke zichzelf respecterende bibliotheek zou het te vinden moeten zijn. Gewoon even vragen aldaar!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 30 mei 2002
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
