WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Boog bepalen door meten van een pijl

Bij het berekenen van een straal van een bocht geldt de formule: r=c²/8p
r= straal
c= de koorde (die de rechte vormt tussen 2 punten op de boog)
p= de pijl gemeten van de rechte naar de boog

Dit, wel te verstaan als de pijl gemeten wordt in het midden van de koorde.
Stel nu, ik meet de pijl niet in het midden maar mechanisch bepaald.
Specifiek : de pijl wordt gemeten op 11.47m van het voorste punt v/d koorde en op 5.68m van het achterste punt.
Kan iemand mij daar de formule van geven ?

Thanks

Nobels
Iets anders - woensdag 23 februari 2005

Antwoord

dag Sven,

Even een correctie op je formule. Volgens mij moet dat zijn:
r = c²/(8p) + ¹/₂p
(als ik het tenminste goed begrepen heb met die pijl)
Deze formule volgt direct uit de stelling van Pythagoras:
(r - p)² + (¹/₂c)² = r²
Maar nu je vraag: het is me niet duidelijk of de pijl radiaal gericht is, of loodrecht op de koorde.
Ik ga maar uit van het eerste geval (radiaal). Je vindt de formule als volgt:
Ik noem x de afstand van het voetpunt van de pijl op de koorde tot het dichtstbijzijnde eindpunt van de koorde.
In jouw geval is dus x = 5.68

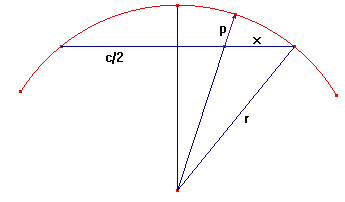
Door twee keer Pythagoras toe te passen, vind je:
(r - p)² = (¹/₂c - x)² + r² - (¹/₂c)²
Hiermee moet je r kunnen berekenen.
Als de pijl toch loodrecht op de koorde staat, dan hoor ik het nog wel. Het wordt dan wel een stuk ingewikkelder.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 februari 2005