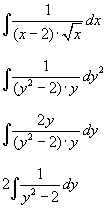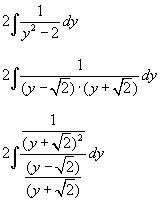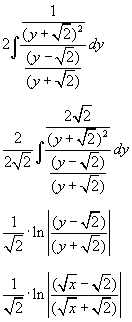WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Primitiveren

hai hai

Gegeven is

1/((x-2)√x)

ik moet alle primitieven hiervan bepalen.
Welke manier kan ik het beste gebruiken?

Groetjes Fleur
Fleur
Student hbo - zondag 20 februari 2005

Antwoord

Beste Fleur,

Ik zou om even van die wortel verlost te zijn beginnen met volgende substitutie:
y = √x $<\Rightarrow$ y² = x

Dan krijg je als integraal:

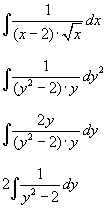
Nu bestaan er in formularia wel standaardintegralen van deze vorm zodat je aan de hand van een formule direct de primieve kan bepalen. Als je hier niet over beschikt of het niet mag/wil gebruiken kan het natuurlijk ook 'met de hand'.

De volgende stappen lijken het moeilijker te maken, dit is dan ook het moeilijkste deel. De noemer kunnen we ontbinden als een verschil van 2 kwadraten. Dan delen we teller en noemer door (y+√2)²

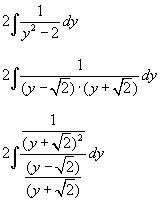
Waarom doen we dit? Als je nu de afgeleide van de noemer berekent, dan bekom je 2√2/(y+√2)². Dit is precies de teller, op die factor 2√2 na. Je kan de teller met deze factor vermenigvuldigen als je voor de integraal corrigeert door te delen door deze factor.
Hierdoor krijgen we een integraal waarbij de teller de afgeleide is van de noemer, met als primitieve ln van de noemer

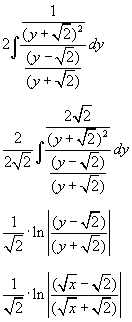
Op het einde gewoon terug gesubstitueerd en je vindt de primitieve

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 20 februari 2005