WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Inhoud van omwentelingslichaam fout

Dit is een reactie op vraag 34191

Beste tom, de oplossing achteraan in mijn boek:
is 136/15 pi;

maar als jij geen fouten meer ziet, en ik geen fouten meer
lijkt het maar twijfelachtig dat het geen typfout zou zijn.

Maar mijn werkwijze is correct, niet?

vriendelijk bedankt
yannic
3de graad ASO - zaterdag 19 februari 2005

Antwoord

Beste Yannick,

In je uitwerking op zich zitten verder geen fouten meer, en zo zou je dus op 16p/15 komen, maar:
Je hebt iets over het hoofd gezien! En eigenlijk, ik dus ook Ik laat het je zien op een figuur:

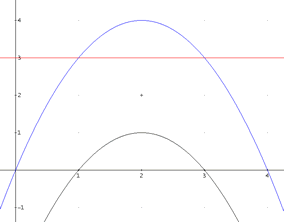
De blauwe functie is de parabool, de rode is de rechte y = 3 en de zwarte is het verschil van deze twee. Door het verschil van de functies te nemen heb je die begrensde top dus naar beneden verschoven. Om de oppervlakte te berekenen is dat prima, die is immers identiek gebleven.

Het omwentelingsvolume is echter verschillend! Als we de zwarte oppervlakte laten wentelen om de x-as krijgen we een soort vervormde bol/rugbybal. Maar als we de oppervlakte begrensd door blauw en rood laten wentelen om de x-as, wat de opdracht was, dan krijg je een soort 'ring', met een veel grotere inhoud!

Hoe kun je dit nu aanpakken?
Je wil dus in het interval [1,3] het omwentelingsvolume van de blauwe - het omwentelingsvolume van de rode.
Dus:
p * ò (1 tot 3) (f(blauw)²-f(rood)²)dx =
p * ò (1 tot 3) ((-x²+4x)²-(3²))dx

Ik heb het even nagerekend en dan kom je op de uitkomst uit je boek. Probeer het hiermee maar even zelf, als je er niet uit geraakt laat je maar wat horen

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 19 februari 2005