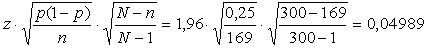WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Steekproef bij populatie van 300

Hallo,
ik heb te maken met het volgende probleem. Ik wil een onderzoek uitvoeren naar klanttevredenheid onder 300 klanten. Wanneer ik dit wil doen met 95% betrouwbaarheid en een maximale fout van 5% krijg ik te maken met de volgende formule:

a= z·Ö((p(1-p))/n). Dit levert voor mij dan op:

5= 1,96*Ö((50·50)/n). Dit levert op dat n 384 is. Dit is meer als 300.

Wanneer ik de eindige populatiecorrectiefactor er op toepas krijg ik:

N/(n+N-1) = 300/(384+300-1)= 0.439

Dit betekent dan weer dat 384 * 0.439 = 168.667

Klopt het dat ik een steekproef moet nemen van 169?

of doe ik iets fout omdat ik met een steekproef (zonder correctie) boven de populatie uitkom?

met vriendelijke Groet, Arjan
Arjan
Student hbo - vrijdag 18 februari 2005

Antwoord

Ja dat is inderdaad iets wat je je af kan vragen. Gelukking kun je nu ter controle vanuit de berekende responsgrootte van 169 terugredeneren of hiermee de marge bij schatting van percentages binnen de gewenste 5% gaat blijven.
Hiertoe kijk je naar de marge bij een betrouwbaarheidsinterval voor fracties en pas je hier de correctie voor eindige populaties op toe.
De gecorrigeerde marge wordt dan:

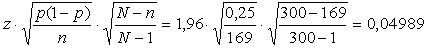
Zoals je ziet klopt dat nu precies. Je blijft inderdaad net binnen die 5% grens. Blijkbaar mag je dus je steekproefgrootteformule zo gebruiken.

Met vriendelijke groet
JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 18 februari 2005