|
|
|
\require{AMSmath}
Kortste weg tussen twee punten over een balk
Hoe kan ik het beste de kortste weg berekenen van punt naar punt. Is hier ook software mogelijk voor mijn TI-83 Basic
Alvast bedankt!!
Tom va
Leerling mbo - dinsdag 15 februari 2005
Antwoord
Neem aan dat we de afstand van D naar F over de zijvlakken van onderstaande balk willen berekenen:
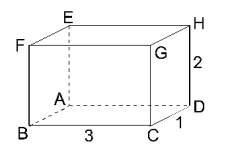
Er zijn nu verschillende mogelijkheden. Je kan via de ribbe EH, via de ribbe CG en nog zo wat...
In zo'n geval is het handig om een 'gepaste' uitslag te tekenen. Hieronder zie je zo'n uitslag:
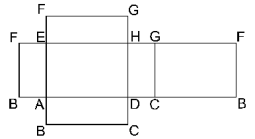
In deze uitslag kan je inderdaad een aantal van die bovengenoemde routes terug vinden:
  
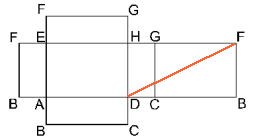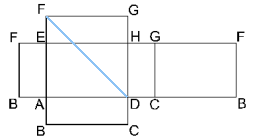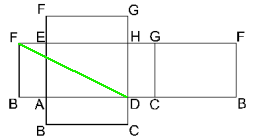
Met behulp van de stelling van Pythagoras kan je de lengten van deze routes wel berekenen. Probleem daarbij is dat je als je over afstand praat wel de 'kortste afstand' bedoelt. Je moet dus wel ALLE mogelijkheden onderzoeken... In bovenstaande uitslag kan je helaas niet ALLE mogelijkheden vinden...
Ik denk dat het 'in prinipe' zondermeer mogelijk moet zijn bij twee gegeven coördinaten een programma te schrijven dat 'automatisch' de gevraagde afstand ophoest. Maar erg eenvoudig wordt dat niet....
Je zou zelfs nog een stap verder kunnen gaan! Je kunt die balk beschouwen als een obstakel in de ruimte. Waarbij je bij twee gegeven punten in de ruimte de afstand zou moeten kunnen bepalen. Nog leuker: je kunt ook allerlei andere objecten gebruiken als bollen, tetraeders enz.
 
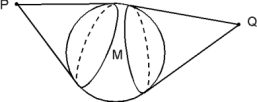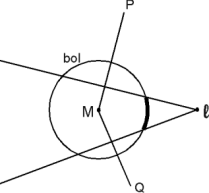
Dan krijg je toch een heel nieuw stukje wiskunde: obstakelmeetkunde... Hierbij spelen golffronten en conflictlijnen misschien nog een interessante rol...
Hopelijk kan je nu verder....
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 20 februari 2005
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
