WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Betrouwbaarheid van een trendlijn

Dit zijn alle waarnemingen die er zijn geweest.Is hier een betrouwbare trendlijn van te maken in Excel. Zo ja welke trendlijn kan je hierbij gebruiken. De linkerkolom geeft het aantal kilo aan die geproduceerd zijn en de rechterkolom geeft het aantal uur aan dat de medewerker nodig had om het aantal kilo te verwerken.

13527 5,34
17349 7,54
19519 7,44
21150 7,51
23097 9,44
23974 10,34
24048 10,83
25039 9,94
25042 10,41
25632 9,66
27370 10,32
28385 10,01
28902 11,34
31703 14,35
32154 13,89

Ik hoop dat u nu voldoende gegevens heeft om een antwoordt te kunnen geven op mijn vraag.

Bijvoorbaat dank,

Bauke
Bauke
Leerling mbo - dinsdag 1 februari 2005

Antwoord

De beantwoording van je vraag heeft even geduurd. Het was nodig om een paar computermodellen op je gegevens los te laten om te kijken wat de beste oplossing is.
Helaas is je oorspronkelijke vraag niet meer beschikbaar in de database.

Allereerst de vraag of een lineair model het beste is:
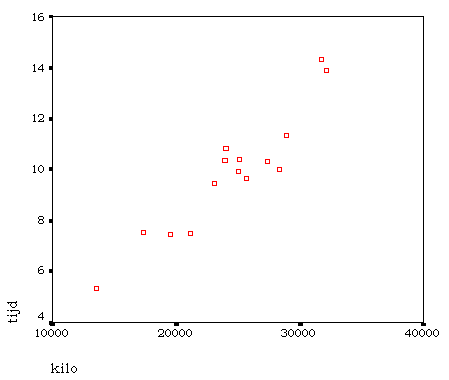
Dat kun je moeilijk zeggen. 15 waarnemingen is daarbij ook niet al te veel zodat bijvoorbeeld een uitschieter ten onrechte het model zou kunnen verstoren. Nu zou je theoretisch een lineair model verwachten. De vraag is of er een reden is om dat lineaire model te verwerpen. Eerst kun je optisch een beeld krijgen door het spreidingsdiagram te bekijken. Hierbij wijst niets erop dat een ander model beter zou zijn dan het lineaire:

Ook een Normal P-P plot kan daar iets meer over laten zien. De punten in een normal P-P plot moeten bij voorkeur zo dicht mogelijk bij de diagonaal zitten. Een patroon in de afwijkingen (bijvoorbeeld eerste helft onder de diagonaal en de laatste helft erboven) zou op een ander model wijzen.

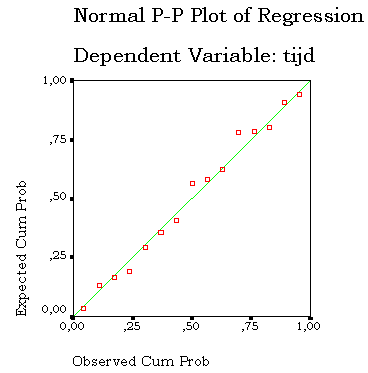
Ook dat doet het dus niet. Ik zie dus geen reden om een ander model dan lineair te gebruiken te meer omdat gevoelsmatig dat model ook lineair zou moeten zijn.
Verder geven de getallen geen reden om hiervan af te wijken.
De regressieformule wordt in dit geval:
benodigde tijd = 0,0004321×kilo's - 0,679
Het enige theoretische bezwaar wat je hierbij zou kunnen aantekenen is dat deze lijn niet door de oorsprong gaat. Maar persoonlijk zou ik daar niet mee zitten.

Ps ik heb geen excel gebruikt voor de berekeningen.

Met vriendelijke groet
JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 februari 2005