WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Berekening in een rechthoekige driehoek

Ik zit met een vraag waar ik niet uit kom
In een rechthoekige driehoek
is hoek ABC=42 graden
En AB =15 CM
BD deelt hoek ABC middendoor

A Bereken AC in mm?

Nick zegt als BD de hoek ABC middendoor deelt, dan zal BD ook het lijnstuk AC wel middendoor delen.

B laat met een berekening zien, of Nico gelijk heeft of niet?
Mensen... Snap hier niks van met die gegevens kan ik niks. Kan iemand mij mischien daar bij helpen?
Nick
Iets anders - zondag 23 januari 2005

Antwoord

Een plaatje.

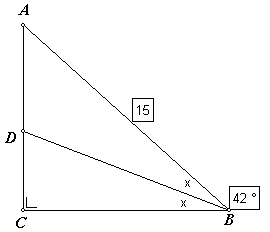
In deze rechthoekige driehoek is de verhouding tussen de zijden AC en AB de sinus van hoek B:
sin(42°) = AC /AB
of
0,6691 = AC / 15
AC = 15 · 0,6691 = 10,0 cm = 100 mm
Nu is in driehoek ABC de zijde BC te berekenen met de stelling van Pythagoras.
Ook driehoek DBC is rechthoekig.
Daarin is de verhouding tussen de zijden DC en BC de tangens van hoek B (van 21°).
Dus
tan(21°) = DC / BC.
En dan kan DC berekend worden.
En dan zal blijken, dat Nick ongelijk heeft.

Overigens, met de bissectricestelling kan je Nicks ongelijk onmiddellijk aantonen.
Er geldt namelijk op grond van die stelling:
AB : BC = AD : CD
Als AD en CD gelijk zouden zijn, dan moet dat ook het geval zijn met AB en BC.
En die zijn in de rechthoekige driehoek ABC zeker niet gelijk (waarom niet?).

Tja, en het kan natuurlijk ook zijn dat hoek A de rechte hoek is in driehoek ABC (maak zelf een bijbehorend plaatje...).
Dan is
tan(42°) = AC / AB, en je kan AC berekenen,
en ook
tan(21°) = AD / AB, en je kan AD berekenen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 januari 2005