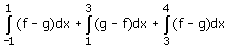WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte berekenen van begrensd gebied

We kregen de volgend opgave:

Bereken de oppervlakte van het gebied, begrensd door de grafieken van f(x)= x³-3x en g(x)=2x²+2x-6 en de verticale lijnen x=-1 en x=4

Aan de grafiek zien we dat een gebied wordt ingesloten tussen [-2,1] door f en g. Ik nam de integraal van f(x)-g(x) over [-2,1] , ik bekwam als oplossing: oppervlakte= 63/4

Helaas is dat niet correct. Ik berekende dan ook nog het ingesloten oppervlak over [-3,-2] Ik berekende de integraal van g(x)-f(x) Ik bekwam als oppervlak=-125/12

Dit optellen bij de eerste oppervlakte krijg ik 16/3...

De juiste oplossing is 343/12 dus waar ben ik de mist in gegaan? Kan iemand van jullie me terug op het juiste pad brengen aub?

Dank bij voorbaat...
Hilde
3de graad ASO - zondag 16 januari 2005

Antwoord

Misschien helpt dit plaatje:

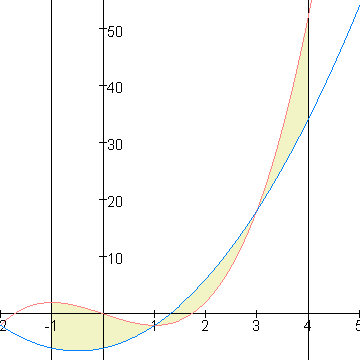
f(x)=rood en g(x)=blauw

Aanwijzing: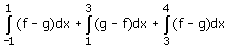

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 januari 2005