WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Berekening hellingsgraad en diameter rechthoek

Als simpele opdracht hebben leerlingen de volgende opdracht meegekregen:
- Kast van 100x200 cm (bxh) moet door een deur met een hoogte van 190 cm.
Vraag: Wat is het hellings-% waarin de kast door de deuropening moet en laat de berekening hiervan zien.

Het antwoord blijft steken op:
- Maximale hoogte kast wanneer deze gekantelt is, is 225 cm (doorsnede)

Deze waarde is verkregen door de kast op de grond te "tekenen" en van hoek tot hoek een meetlat te leggen.... Hier moet toch wel een formule voor zijn?

Voor wat betreft de hoek hebben we geen idee hoe dit te berekenen is.

Kunt u helpen?

MVG
Marcel
Ouder - vrijdag 14 januari 2005

Antwoord

Dag Marcel,

Ik neem aan dat de deur smaller is dan 1 meter, anders zou je namelijk de kast nog over de breedte kunnen kantelen, maar dan moet je weer weten hoe diep de kast is.
Verder neem ik aan dat de diepte van de kast kleiner is dan de breedte van de deur, anders kan hij er helemaal niet door.
Nu gaat het niet om de maximale hoogte die de gekantelde kast bereikt, maar om de hoek waaronder gekanteld moet worden zodat de kast juist 190 cm hoogte bereikt.
Dit kan uit het volgende plaatje berekend worden:

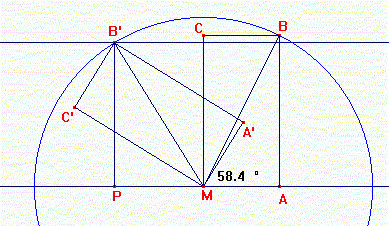
Het gaat om hoek AMA'.
De afstand van B' tot P is gelijk aan 190 cm. De rechtopstaande kast steekt daar dus 10 cm bovenuit.
Kun je de straal van de draaicirkel berekenen? Denk aan Pythagoras.
Verder geldt:
$\angle$AMA' = 180° - $\angle$PMB' - $\angle$B'MA'
$\angle$B'MA' kun je berekenen met de inverse tangens.
$\angle$PMB' kun je berekenen met de inverse sinus; gebruik daarvoor de straal van de draaicirkel.
Hieruit kun je dus de gevraagde hoek berekenen.
Als het goed is, kom je uit op 58.4°
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 14 januari 2005