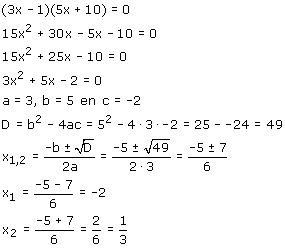WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Het oplossen van een vergelijking

Ik snap deze som niet:

(3x-1)(5x+10)=0

Ik heb de haakjes weggehaald en ik gebruik vervolgens de abc-formule. Maar mijn antwoord klopt niet met dat van het antwoordenboekje. En het is ook geen fout van het antwoordenboekje (althans, dat zegt mijn leraar)
Jannie
Leerling bovenbouw havo-vwo - woensdag 12 januari 2005

Antwoord

Deze vraag leidt tot 2 leermomenten!

1.
Probeer bij het oplossen van vergelijkingen te begrijpen waar je mee bezig bent. Dat is namelijk veel handiger dan een soort 'vaststaand riedeltje' afwerken...

2.
Kennelijk gaat het oplossen met de ABC-formule niet goed! Dus nu heb je een standaard oplossing, maar dan gaat het nog fout!

We gaan er maar eens op in!

Eén van de eerste dingen die je leert bij het oplossen van tweedegraads vergelijkingen is ontbinden in factoren. Een hele handige manier om tweedegraads vergelijkingen op te lossen waar mooie oplossingen uitkomen. Op 1. Ontbinden in factoren kan je dat nog eens nalezen.

Het doel van dat ontbinden in factoren was dat je ergens op een punt komt waarbij er in je vergelijking iets staat als:

...×...=0

Waarom? Als a·b=0 dan geldt: a=0 of b=0. Hierdoor krijg je dan twee nieuwe (eerstegraads) vergelijking die je dan kan oplossen. Zie 1. Een eenvoudige vergelijking oplossen om dat nog eens na te lezen.

Jouw vergelijking staat al precies in die vorm! Dus eigenlijk ben je raar bezig als de haakjes gaat wegwerken, gelijksoortige termen samen neemt, op nul herleid, probeert te ontbinden en dan toch maar de ABC-formule zou willen gaan gebruiken!

Kijk maar eens goed zoals het gaat:

(3x-1)(5x+10)=0
3x-1=0 of 5x+10=0
3x=1 of 5x=-10
x=¹/₃ of x=-2

En klaar is Klara! Dus veel simpeler dan je wellicht dacht. Een leermoment zou ik zeggen...

2.
Stel je nu eens voor dat je in een vlaag van verminderd inzicht toch de haakjes wegwerkt en de ABC-formule zou gebruiken... dan moeten er natuurlijk wel dezelfde oplossingen uit komen, anders doe je iets fout! Dat zal hieronder dan nog eens doen voor je...

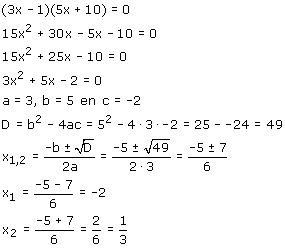
..en nu nog maar eens kijken of je alle stappen snapt en zelf zou kunnen maken... en kijk nog even naar je eigen uitwerking en leer van je fout(en). Dat is dan het tweede leermoment...

Succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 januari 2005