WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs van de stelling van Pythagoras

Ik heb al vele bewijzen in verband met Pythagoras opgelost (Euclides, J. A. Garfield, ...), maar bij dit bewijs zit ik helemaal vast! Ik zou niet weten hoe ik eraan zou moeten beginnen. Ik heb al overal op internet gezocht en blijkbaar is dit een bewijs van Bill Casselman (in mijn cursus staat: indisch puzzelbewijs). Op deze site: http://www.cut-the-knot.com/pythagoras/index.shtml (zie 'proof 27') heb ik al wat hints gevonden, maar toch slaag ik er niet in de oefening op te lossen! ik heb al dingen gezocht rond middelevenredigheden en evenredigheden, maar op deze manier kom ik er niet, ook door met hoogtelijnen te werken vind ik geen oplossing.
Annele
Student Hoger Onderwijs België - dinsdag 4 januari 2005

Antwoord

Bewijs 26 en 27 van je bovenvermelde website komen eigenlijk op het zelfde neer.

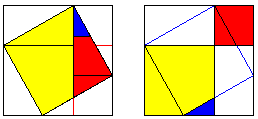
Bewijs 26:

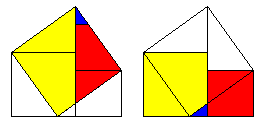
Bewijs 27:

Enkel en alleen met congruente driehoeken kan je dit heel eenvoudig aantonen. vb.
Het gele driehoekje is congruent met de driehoek bestaande uit het rode trapezium samen met de blauwe driehoek want de kleinste scherpe hoek van de blauwe driehoek is gelijk aan de kleinste scherpe hoek van de gele driehoek, de schuine zijde van beide driehoeken zijn gelijk (ze vormen immers samen met de grootste scherpe hoek van de gele driehoek een rechte hoek = een hoek van 90°) en analoog zijn ook de grootste scherpe hoeken gelijk. We hebben dus het congruentiegeval HZH (Hoek-zijde-hoek).
Van twee congruente driehoeken weten we dat alle corresponderende zijden gelijk zijn, en alle corresponderende hoeken zijn eveneens gelijk.

Je hebt nu onder andere ook al dat de lengte van de zijde van het gele (met blauw) gekleurde vierkant in de rechtse figuren gelijk is aan de langste rechthoekzijde van de gele driehoek,
en dat de lengte van de zijde van het rode vierkant in de rechtse figuren gelijk is aan de lengte van de kortste rechthoek zijde van de gele driehoek. En daar herken je de stelling van Pythagoras.

Wat je nu zelf nog moet aantonen is dat die driehoekjes ook effectief passen in de grijze vakken. Maar dit gaat volledig analoog door congruentie.

Ik hoop dat dit een antwoord was op je vraag.

Met vriendelijke groeten,
Els

Els

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 januari 2005