|
|
|
\require{AMSmath}



Variërende inhoud van een piramide
Hoi, ik heb een vraag waar ik zelf niet uit kom,
De inhoud van een piramidevormige silo (met de punt naar beneden) is: 10. De silo wordt gevuld met graan. Geef aan de zijkant aan hoe hoog het graan staat als de silo voor 1/5, voor 2/5, voor 3/5 en voor 4/5 deel gevuld is. De uitstroomopening onderin de piramide mag verwaarloosd worden.
De hoogte van de piramide is: 2
het grondvlak van de piramide is vierkant.
de inhoud van de piramide berekenen kon ik wel, dat is 1/3.grondvlak.hoogte=10
1/3.grondvlak.2=10 ®grondvlak is 15 dus de randen zijn elk Ö15
dus nu heb ik het voor 5/5 uitgerekend, maar om het voor 1/5,2/5,3/5,4/5, dat lukt me niet, omdat dan het grondvlak gaat varieren en de hoogte ook...
Bernar
Student hbo - woensdag 29 december 2004
Antwoord
Eerst maar eens een tekening:
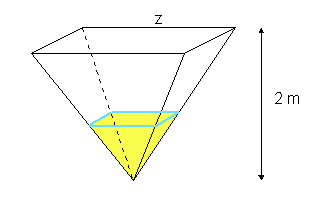
Nemen we even aan dat er nu nog 1/5 van de totale inhoud in de silo zit. De kleine en de grote piramide zijn gelijkvormig. Dat betekent dat als de inhoud van de grote piramide 5 keer zo groot is dan de inhoud van de kleine piramide dat de lengten van de grote piramide een 3Ö5 keer zo groot zijn dan de lengten van de kleine piramide.
Daarmee zou je dit probleem moeten kunnen oplossen! Denk er maar over na...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 29 december 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|











