|
|
|
\require{AMSmath}



Bereken de kans dat men geen aas krijgt
situatie:
iedere speler ontvangt 13 kaarten uit een boek van 52 kaarten (4 asen). bereken de kans dat men geen aas krijgt.
ik ben er niet zeker van maar ik denk dat dit het antwoord is:
(1-4/52)*(1-4/51)....(1-4/40) = ongeveer 1/606
immers, bij de eerste trek is de kans dat men geen aas krijgt + de kans dat men wel een aas krijgt gelijk aan 1.
X + 4/52 = 1
bij de volgende trek
X + 4/51 (kaart weg) = 1
enzoverder.
ik vind nergens het antwoord, dus vraag ik het hier.
danku
roeb
Leerling bovenbouw havo-vwo - woensdag 15 december 2004
Antwoord
De kans dat je bij 13 kaarten uit een volledig kaartspel geen aas krijgt kan je zo berekenen:
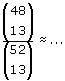
Je kunt dit lezen als 'het aantal manieren om 13 kaarten te kiezen uit de 48 niet azen' gedeeld door 'het aantal manieren om 13 kaarten uit 52 te kiezen'.
Zie ook: 5. Hypergeometrische verdeling

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 december 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|