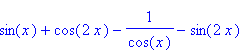WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Tan(x)=sin(x) cos(2x)-1/cos(x)-sin(2x)

Die haakjes heb ik zelf 'bedacht', dat ging al eerder ook eens mis. Kun je me misschien wat tips geven daarover? Ik zet die haakjes blijkbaar vaker verkeerd. Wat is de 'regel' voor haakjes?

De opgave zoals in het boek staat is: sinx + cos2x - 1 / cosx - sin2x = tanx, is dat wel aan te tonen en zo ja, hoe? En welke productformule voor cos2x moet je in welke situatie toepassen?

gr. J
J.
Student universiteit - woensdag 15 december 2004

Antwoord

dag Jaap,

Uit je toelichtende mail bleek, dat alles wat voor de deelstreep staat tot de teller behoort, en alles wat na de deelstreep staat tot de noemer behoort.
Dit geef je het beste aan met haakjes:
(sin(x) + cos(2x) - 1)/(cos(x) - sin(2x))
Als je die haakjes niet plaatst, dan zou je het linkerlid van de formule moeten interpreteren als

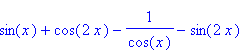
Maar nu het antwoord op je vraag.
Gebruik cos(2x) = 1 - 2·sin²(x)
Dan wordt de teller:
sin(x) + 1 - 2·sin²(x) - 1 = sin(x) - 2·sin²(x) = sin(x)·(1 - 2·sin(x))
en de noemer wordt:
cos(x) - 2·sin(x)·cos(x) = cos(x)·(1 - 2·sin(x))

Zie je nu de gemeenschappelijke factor in teller en noemer? Snap je dat je deze kunt wegdelen? En dat je dan juist tan(x) overhoudt?
Kortom: een kwestie van 'buiten haakjes brengen'.

succes verder,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 december 2004