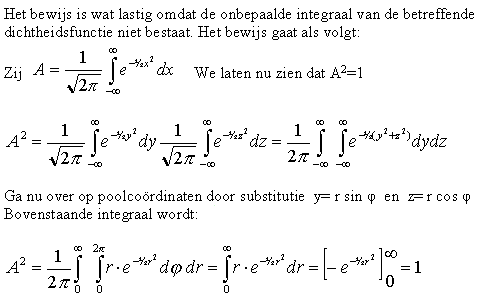WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte onder de Gausscurve

Kan iemand mij een waterdicht bewijs leveren dat aantoont dat de integraal van -¥ tot +¥ onder de Gauss Curve gelijk is aan 1? Zelfs in cursussen Analyse en Statistiek van de universiteiten vind ik geen bewijs terug...
Dus bewijs dat: ò van -¥ tot +¥ gelijk is aan 1
Sorry, ik ben vergeten te vermelden dat het de berekening was van y = e^(-x²)

Dank bij voorbaat :) het zou mij erg veel vooruit helpen
Freder
Leerling bovenbouw havo-vwo - maandag 29 november 2004

Antwoord

Tjonge jonge, die universiteiten van tegenwoordig ook. En zo heel moeilijk is dat echt niet. Je moet een beetje van poolcoordinaten weten etc. Okay, hier komt het, snap je het dan prima, snap je het niet laat het dan maar zitten.

Dus ook A=1
Dit alles in het geval van een standaardnormale verdeling.

Het algemene geval is ook zo te bewijzen na de standaardiseringssubstitutie.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 29 november 2004