WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kortste pad probleem

Gegeven : een bol met middelpunt (0,0,0) en straal r1 en een cilinder met middellijn gaande door (0,0,0) en straal van de dwarsdoorsnede r2. (dus vergelijking van beide gekend).

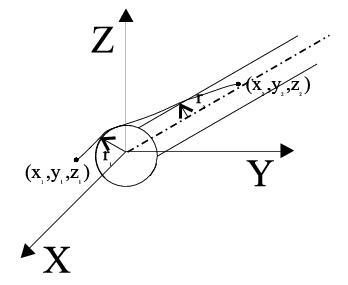
Gevraagd : De lengte van het korste pad tussen een willekeurig punt (x1,y1,z1) en een punt op het cilinderoppervlak (x2,y2,z2).
amaryl
Docent - donderdag 25 november 2004

Antwoord

Dus het punt P(x1,y1,z1) moet op de bol liggen, het punt Q(x2,y2,z2) op de cilinder, en de route moet over het oppervlak lopen.
Interessant!
Ik neem aan dat de richting van de as van de cilinder ook bekend is.
Intuïtief zou ik zeggen: loop van P naar een punt X op de snijcirkel, (kortste route via een grote cirkel van de bol), en van de snijcirkel naar Q via een kromme die je kunt uitrollen tot een recht lijnstuk, als je begrijpt wat ik bedoel.
Enige vraag is dus nog: welk punt X op de snijcirkel levert de kortste route?
Je kunt de coördinaten van X met één parameter x weergeven (uitgedrukt in r1 en r2).
Vervolgens druk je de afstand van P tot X en van X tot Q uit in deze parameter x, en de som hiervan minimaliseer je met behulp van differentiëren.
Zou dat lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 30 november 2004

Re: Kortste pad probleem