WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Arccos en arcsin met behulp van arctan

Dit is een reactie op vraag 4473

Hallo kun er iemand wat meer uitleg geven ontrent de manier waarop je aan ArcCos:=-ArcTan(r/SQRT(-r*r+1))+0.5*pi komt zoals in de eerder beantwoorde vraag. De bedoeling is om hetzelfde te doen voor een arcsinus.

Ik had oa het volgende al geprobeerd (voor Arccos):
Arccos(r)= Arctan(r)*Fx ; (Fx=correctiefaktor),
=Fx= Arccos(r)/Arctan(r)
=Fx/1= Arccos(r)/Arctan(r)
= cos(Fx)/Tan (1)=r/r =1 (correct??...)
=(cos(Fx)*cos(1))/sin (1) =1
complementaire hoeken sin x= cos( (pi/2)-x)
=(cos (Fx)*cos(1))/cos ( (pi/2)-1) =1
hoe verder? is dit wel correct?
Bedankt alvast voor alle hulp
wimpie
Student Hoger Onderwijs België - zondag 21 november 2004

Antwoord

Iek.... je doet rare dingen!!

Misschien kan je beter even naar dit stukje eenheidscirkel kijken:

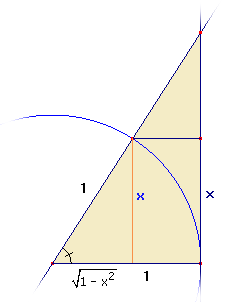
Welke hoek hoort er bij een sinus van x? Oftewel: wat is de tangens van die hoek? Niet echt ingewikkeld toch?

Voor de volledigheid: in Pascal zou het er zo uit zien:
FUNCTION ArcSin(r:REAL):REAL;
   BEGIN
      ArcSin:=0;
      IF (r1) OR (r-1) THEN EXIT;
      IF Gelijk(r,1) THEN ArcSin:=pi/2
      ELSE IF Gelijk(r,-1) THEN ArcSin:=3*pi/2
      ELSE ArcSin:=ArcTan(r/SQRT(-r*r+1))
   END;
Hopelijk heb je er iets aan.
Zie Inverse Sine

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 november 2004