WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructie gelijkzijdige driehoek in driehoek

Gegeven is een driehoek ABC.
Contrueer een gelijkzijdige driehoek PQR, zodat P op AB, Q op BC en R op CA ligt.
Peter
Student hbo - dinsdag 7 mei 2002

Antwoord

Beste Peter,

Construeer gelijkzijdige driehoeken op elk van de zijden van ABC die alledrie naar buiten gericht zijn. Verbind elke nieuwe top met het overstaande hoekpunt van ABC. De drie lijnen die je dan krijgt gaan door één punt (het 1^e punt van Fermat-Torricelli), in de figuur is dat G. Trek vanuit dit punt loodlijntjes naar punten H, I en J op de zijden van ABC. De omgeschreven cirkel van HIJ snijdt de zijden van ABC in nog drie punten, de gevraagde punten PQR.

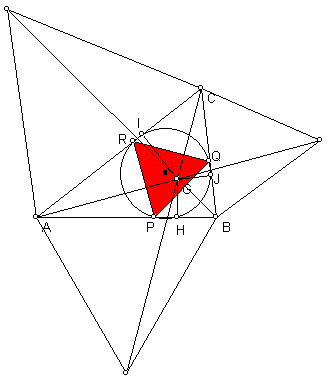
Je kunt meer variaties van deze punten construeren. Trek bijvoorbeeld de lijn door P loodrecht op AB, en evenzo loodlijntjes door Q en R. Deze lijnen ontmoeten elkaar in een punt X (dit heet de isogonale verwant van het eerdere punt G). Draai je nu de lijnen XP, XQ en XR allemaal over dezelfde hoek tussen -90° en 90° om X, dan snijden deze lijnen de betreffende zijden weer in punten P'Q'R'. Deze punten vormen weer een gelijkzijdige driehoek.

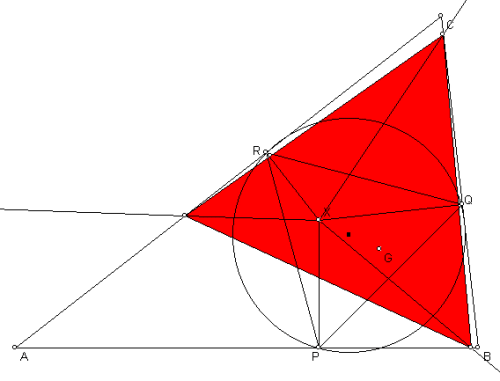
Tenslotte kun je in plaats van de naar buiten gerichte gelijkzijdige driehoeken waar we mee begonnen, ook de gelijkzijdige driehoeken naar binnen gericht laten zijn.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 7 mei 2002

Re: Constructie gelijkzijdige driehoek in driehoek