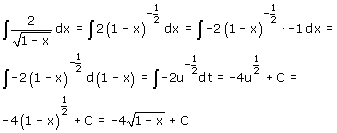WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Primitieve van een wortelfunctie

Het betreft de opgave 15 j, par. 3.2 van NGNT5 van Getal en Ruimte, blz 102.

de functie is: j(x)= 2/(Ö(1-x))
j(x)= 2(Ö(1-x))^-1
j(x)=2(1-x)^-.5

J(x)=a*2(1-x)^.5
J(u)=a*u^.5 u(x)=2(1-x)
J'(x)= .5*a*u^-.5 *u'(x)
J'(x)= .5*a*2(1-x)^-.5 *u'(x)
J'(x)= a(1-x)^-.5 *u'(x)

Nu is mijn vraag: wat is u'(x).
is dat:
a) -1
b) -2

mijn redenatie voor b is:
u(x)=2(1-x)
u(x)=2-2x
u'(x)=-2

mijn redenatie voor a is:
in de totale formule word de halfde macht van het deel
(1-x) genomen. Dus daarom zou je in u(x) de x niet buiten haakjes moeten halen. Is dat waar of niet? oftewel: is antwoord a, of antwoord b juist?

Rajiv
Leerling bovenbouw havo-vwo - zondag 7 november 2004

Antwoord

't Is rommelig! Om dit soort verwarring te voorkomen is het niet verkeerd om bij de substitutiemethode je te houden aan een 'standaard' berekening. Je krijgt dan iets als:

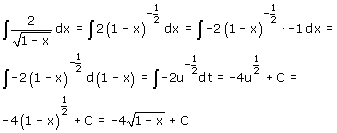
Een heel gedoe voor iets wat natuurlijk ook een stuk sneller kan, maar zeker in het begin niet verkeerd. Ik zie tenminste nergens 'punten' van onduidelijkheid!

Uiteraard kan je je antwoord altijd controleren door te differentiëren!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 7 november 2004