WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe moet ik de verschiltoets voor gemiddelden toepassen?

Ik ben bezig met mijn profielwerkstuk, waar ik al eerder een vraag voor heb ingestuurd, het gaat om een tweelingenonderzoek waarbij ik kijk naar de overeenkomsten in intelligentie bij eeneiige tweelingen. Ik heb oa het IQ getest. JaDex had mij eerder geholpen en adviseerde ook broers of zussen of tweeeiige tweelingen te testen, ik heb nu een heel aantal tweeeiige tewelingen getest. Hij zei toen dat ik daarvoor de verschiltoets voor gemiddelden kon gebruiken, maar ik heb geen inforamtie over die toets omdat wij op school en in de bieb niet over statistiek boeken beschikken, in ieder geval nauwelijks.
MIjn vraag was of jullie mij kunnen helpen, of heeft de toets soms een andere naam, dan kan ik het makkelijker zoeken..

Ik hoop iets van jullie te horen
Marjan
Leerling bovenbouw havo-vwo - vrijdag 29 oktober 2004

Antwoord

Okay, we maken een eind aan het verhaal.
Je hebt het vermoeden dat intelligentie (voor een deel) genetisch bepaald is. Wanneer dat zo is zal het verschil in intelligentie bij eeneiige tweelingen kleiner zijn dan bij twee-eiige tweelingen. En dat wil je graag toetsen.
Dat is dus een eenzijdige toets voor gemiddelden.
De nulhypothese H₀ hierbij is dat er in werkelijkheid geen onderscheid is.
De alternatieve hypothese H₁ is dat het verschil bij eeneiige tweelingen kleiner is.
Dat betekent H₀: m₂=m₁ (er is geen onderscheid)
H₁: m₂m₁ Û m_v=m₂-m₁0 (kleinere verschillen bij een-eiige tweelingen)
1: staat voor de groep eeneiige tweelingen
2: staat voor de groep twee-eiige tweelingen
De laatste regel geeft aan dat het verwacht gemiddelde (van de verschillen) bij tweeeiige tweelingen groter zal zijn dan bij eeneiige tweelingen.
Bij de steekproefgemiddelden klopt dat wel. Kijk zelf maar.

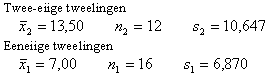
Nu is de vraag of dit verschil significant is of ook van het toeval afhankelijk kan zijn. Om te berekenen vanaf waar een verschil significant is hebben we nodig:
De onbetrouwbaarheid van de toets: omdat je een kleinschalig onderzoekje hebt zou ik 10% kiezen.
Vervolgens zijn er meerdere soorten verschiltoetsen. Welke je moet nemen hangt af van de standaarddeviaties in beide groepen (10,647 en 6,870). Omdat deze nogal verschillen neem je de verschiltoets voor gemiddelden waarbij je aanneemt dat de standdaarddeviaties verschillend zijn:
als gevolg hiervan bereken je de standaarddeviatie bij de verschilvariabele met:

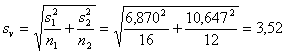
Ook als gevolg moet je de t-waarde (eenzijdig) uit de students t verdeling baseren op de kleinste steekproef. Deze steekproef heeft grootte 12. Dat betekent dat bij de t waarde je moet uitgaan van 11 (=n-1) vrijheidsgraden. Verder moet je de t-waarde baseren op 90% betrouwbaarheid, eenzijdig. Dat levert op t₁₁ = 1,80.
De grens van het kritiek gebied bij deze toets is nu t₁₁·s_v=1,80·3,52=6,3
Dit betekent dat een verschil in gemiddelden tot 6,3 nog aan het toeval kan liggen. Echter in je steekproef is het verschil al 6,5. Dat ligt niet aan het toeval en hiermee heb je dus het verschil statistisch aangetoond.
Conclusie uit dit alles is: het verschil in intelligentie bij eeneiige tweelingen is kleiner dan bij twee-eiige tweelingen.
En dat is waar je naar toe wil

Dat is eigelijk het verhaal. Alles nog even narekenen uiteraard. Het ziet er wellicht wat anders uit dan die link die ik je per mail gegeven heb, maar komt wel op hetzelfde neer. Ik hoop dat dit een beetje te begrijpen is.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 november 2004

Re: Hoe moet ik de verschiltoets voor gemiddelden toepassen?