WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Stelling van Pythagoras

Dit is een reactie op vraag 27887

Na goed kijken naar de tekening, en zelf tekeningen gemaakt te hebben, ben ik uiteindelijk op dit bewijs gekomen. Volgens mij klopt het, maar ik hoop dat u het voor de zekerheid even wil checken. Erg bedankt voor uw hulp, zonder hulp was het niet gelukt, maar door mij zelf ook na te laten denken heb ik toch ook wat gedaan. Bedankt

Als je BC verlengt en dan vanuit het verlengde een loodlijn trekt naar D, krijg je een nieuwe driehoek, BED. Driehoek BED congrueert met driehoek ABC. Dus:
BC = DE = zijde a

Dan kijken we naar de driehoeken BDI en BDC. Deze driehoeken hebben dezelfde basis (BD) en dezelfde hoogte, immers liggen C en I beide op een lijn (CF) evenwijdig met BD
Zodat opp(BDI) = opp (BDC).
We nemen BC als basis en DE als hoogte. Al eerder hebben we gezien dat BC = DE = a, dus:
Opp (BDC) = ¹/₂ x DE x BC = ¹/₂ x a x a = ¹/₂ a²
Driehoek BDI is de helft van rechthoek BDFI (DI is een diagonaal), zodat
opp(BDFI) = 2 x ¹/₂ a² = a²

Als je AC verlengt en dan vanuit het verlengde een loodlijn trekt naar H, krijg je een nieuwe driehoek, AHK. Driehoek AHK congrueert met driehoek ABC. Dus:
HK = AC = zijde b

Dan kijken we naar de driehoeken ACH en AHI. Deze driehoeken hebben dezelfde basis(AH) en dezelfde hoogte, immers liggen C en I op een lijn (CF) evenwijdig met AH.
Zodat opp(AHI) = opp(ACH)

We nemen AC als basis en HK als hoogte. Al eerder hebben we gezien dan HK = AC = b,dus:
Opp (ACH) = ¹/₂ x AC x HK = ¹/₂ x b x b = ¹/₂ b²
Driehoek AHI is de helft van rechthoek AFHI (HI is een diagonaal), zodat
Opp (AFHI) = 2x ¹/₂ a² = a² ...(1)
Nu kunnen we een optelsom maken en de oppervlakte berekenen van ABDH
Opp (ABDH) = c²
Opp (BDFI) = b² ...(2)
Opp (AFHI) = a² ...(3)
Opp (ABDH) = opp (BDFI) + opp (AHFI) c² = a² + b²
Nu ben je dus uitgekomen op de stelling van Pythagoras

Marlee
Leerling bovenbouw havo-vwo - zaterdag 16 oktober 2004

Antwoord

Dag Marleen,

Allereerst nog maar even een plaatje (voor andere lezers van WisFaq).

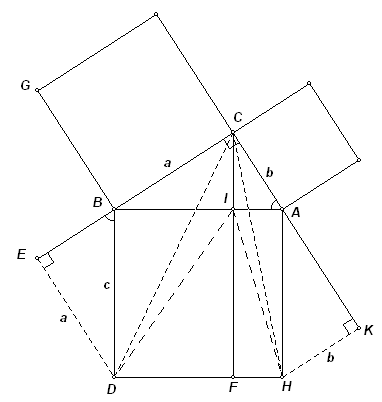
Na correctie van een enkele verschrijving is het door jou gegeven bewijs juist.
Zie de regels die ik in je bewijs (hier boven) heb aangegeven met (1), (2), (3). Deze regels moeten luiden:

(1) Opp (AFHI) = 2 x ¹/₂ b² = b²
(2) Opp (BDFI) = a²
(3) Opp (AFHI) = b²

Verder goed gedaan!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 18 oktober 2004