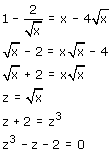WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: De oplossing van twee functies

Dit is een reactie op vraag 28053

Hey :),

Ik heb heel wat geprobeerd, en het volgende is er uit komen vallen, maar verder wil het niet:

f'(x) = f(x)
1-2/Öx = x-4Öx
1-2 = (x-4Öx) · Öx
-1 = x^1,5 - 4x
Ik wil de x achter 4 weg, dus ik ga links en rechts delen door x.
-1/x = (x^1,5 - 4x) / x
-1/x = x^0,5 - 4
-1 · x^-1 = x^0,5 -4
-1 + 4 = x^0,5 / x^-1
3 = x^1,5

Wat kan de volgende stap zijn? Is het wel juist wat ik doe? zo ja, kan het nog korter via een andere weg?
Alvast dank.
Groeten,
Hans
Leerling bovenbouw havo-vwo - zondag 3 oktober 2004

Antwoord

Volgens mij ga je in derde regel uit de bocht... Als ik je uitwerking daar op pik kom ik op:

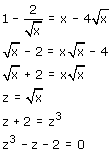
Maar ja wat dan?

Maar eh... er staat bereken op 1 decimaal... waarom gebruik je niet gewoon je GR om de oplossing te benaderen?

P.S.
Je schrijft:
-1 · x^-1 = x^0,5 - 4
en dan:
-1 + 4 = x^0,5/x^-1
Moet je die 4 niet ook delen door x^-1 dan?
Ja dus... maar dan krijg je gewoon je 4x weer terug....

...en dan nog iets:

Als je van:
1 = x^1,5 - 4x
uiteindelijk na vele omzwervingen uitkomt op:
3 = x^1,5
zou je je toch even op 't hoofd moeten krabben, want nu lijkt het net of.... o ja natuurlijk! Dat kan nooit goed zijn...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 oktober 2004