WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Staartdeling en gebroken vergelijking

Ik moet de volgende gebroken vergelijking oplossen:
(6x²-13x+6)/(3x-2)=0
Het antwoord zou moeten zijn:
M.b.v. een staartdeling vinden we: 2x-3=0 zodat x = 3/2
Kunt u mij deze vergelijking uitleggen en tevens uitleggen hoe een staartdeling precies in zijn werk gaat?
Alvast hartstikke bedankt
Mloes
Leerling bovenbouw havo-vwo - woensdag 29 september 2004

Antwoord

Het is niet nodig deze vergelijking met een staartdeling op te lossen: een breuk is nul als de teller nul is en de noemer niet.
In jouw voorbeeld betekent dit dat je de gegeven vergelijking kunt vervangen door
6x²-13x+6=0 en 3x-2¹0
De vergelijking 6x²-13x+6=0 kun je oplossen (b.v. met de abc-formule), je krijgt dan x=³/₂ of x=²/₃.
Maar: als x=²/₃ dan is 3x-2 gelijk aan nul.
Er blijft dan over: x=³/₂.

Met een staartdeling gaat het oplossen zoals in onderstaand plaatje:

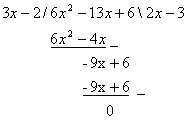
Je begint met 2x(3x-2) dat levert 6x²-4x.
Dit trek je af van 6x²-13x+6. Je houdt over -9x+6.
Dit is precies -3(3x-2)
Dus haal je van -9x+6 -3(3x-2) af.

Conclusie: ^6x²-13x+6/_3x-2=2x-3
Je lost nu op 2x-3=0, dus x=3/2

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 30 september 2004