WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Grootste kijkhoek bepalen

Ik heb een vraag dat ik niet kan beantwoorden. het gaat zo: een beeldhouwwerk met hoogte H m staat op een voetstuk met hoogte H' m, op welke afstand van het voetstuk wordt het beeldhouwwerk onder een zo groot mogelijke hoek gezien. Ten eerste begrijp ik de vraag niet zo goed, ten tweede heb ik geen idee hoe ik aan zo'n vraagstuk moet beginnen antwoorden. kunt u me aub raad geven een de juiste manier om het op te lossen?
Liat L
3de graad ASO - vrijdag 17 september 2004

Antwoord

Dag Liat Lavan

Er zijn verschillende manieren om uw probleem aan te pakken. De één is al wat eenvoudiger dan de andere. Ik zal u één mogelijke manier toelichten. We gaan er van uit dat de ogen van de persoon die het standbeeld bekijkt op een hoogte z staan (zie tekening).

Er zijn twee mogelijkheden. Als zh, dan moet de persoon zo dicht mogelijk bij het standbeeld gaan staan (x@0), om een zo groot mogelijke hoek te bekomen. Die hoek is net ietsje kleiner dan 180 graden. Als zh, moeten we de gevraagde afstand x wiskundig uitrekenen. De situatie waarbij zh ziet u op onderstaande tekening:

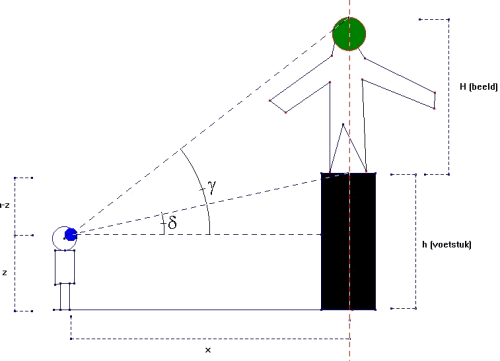
We moeten de waarde voor x zoeken, waarvoor de hoek a maximaal is. Dit is hetzelfde als de waarde voor x zoeken waarvoor de tangens van a maximaal is. Want hoe groter a, hoe groter tan(a)! We proberen dus tan(a) te schrijven in functie van x (om daarna met de afgeleide het extremum te kunnen bepalen). Dit alles kan aan de hand van onderstaande goniometrische formule:

tan(a)=tan(g-d)=^{tan(g)-tan(d)}/_{(1+tan(g)*tan(d))}

Deze formule schrijft tan(a) in functie van enkele andere tangensen. De waardes van deze tangensen kunnen we afleiden uit de tekening. De tangens is immers de overstaande zijde gedeeld door de aanliggende zijde in een rechthoekige driehoek.

tan(g)=^(H+h-z)/_x
tan(d)=^h-z/_x

We stellen tan(a)=y. Dan kunnen we tan(a) schrijven als:

y=^x*H/_{(x²+(h-z)*(H+h-z))}

Nu rest ons alleen het maximum te zoeken van deze functie. De gevonden x is dan de afstand van waar op je het beeldhouwwerk onder een zo groot mogelijke hoek ziet. Probeer dit maximum zelf even te zoeken.

Groetjes en veel succes

Igor

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 17 september 2004