WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Parabool (loodlijn, raaklijn, brandpunt)

opgave:
F is een brandpunt van P - y²=2px. De loodlijn L in F op de as van de parabool snijdt P in q en r. De normaal in q snijdt P een tweede keer in s.
Bewijs dat de raaklijn in q, de evenwijdige door r aan de X-as en de raaklijn in s door één punt gaan .

Ik heb eerst een overzichtelijke figuur gemaakt en als oplossingsmethode het volgende gevonden:

stelsel vormen van de raaklijn door Q (1) en de evenwijdige met de x-as door R (2) en de raaklijn door S (3)

(1) y.yq=p(x+xq)
(2) y=r
(3) ysy=p(x+xs)

En wat nu gezongen? Dat kun je toch niet combineren met elkaar? Of wel? (het zou moeten van wel...)

Kan iemand me verder helpen? Ik heb morgen helaas test hierover...

Dank!

Wendy
3de graad ASO - dinsdag 14 september 2004

Antwoord

Hallo Wendy

Mijn antwoord is gebaseerd op onderstaande tekening. U zal de betrokken rechten wel herkennen.

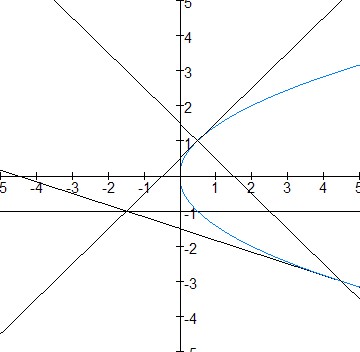
(getekend voor p=1)

We zoeken de vergelijking van alle raaklijnen:

a) raaklijn 1

Het brandpunt van deze parabool is (0,^p/₂), dat heb je ongetwijfeld wel geleerd (standaardformuletje).

We zoeken dus de rechte die raakt aan de parabool in x=^p/₂.

Er bestaat een formule voor de raaklijn aan een parabool. De raaklijn aan een parabool in het punt (x₀,y₀) is

y * y₀ = p * (x + x₀ )

(uit je vraagstelling leid ik af dat je deze kent)

De raaklijn in Q wordt dan:

y= x + ^p/₂

b) raaklijn 2

De vergelijking van deze raaklijn is y=-p (eenvoudig te vinden)

c) raaklijn 3

We zoeken de vgl van de normaal aan de parabool in x=^p/₂. De normaal staat loodrecht op "raaklijn 1" (zie boven). De richtingscoëfficiënt van "raaklijn 1" is 1. Dus is de richtingscoëfficiënt van de normaal -1.

(dit volgt uit: als twee rechten loodrecht op elkaar staan, dan is het product van hun richtingscoëfficiënten =-1)

We weten ook dat die normaal door het punt Q gaat en de coordinaten van Q zijn gekend. Aangezien nu zowel de richtingscoëfficiënt als een punt van de normaal gekend zijn, kan men de vgl van de normaal vrij gemakkelijk opstellen. De vergelijking wordt (controleer zelf eens):

y=³/₂*p - x

Bepaal vervolgens de snijpunten van de normaal met de parabool.

Stelsel:

y²=2*p*x
y=³/₂*p - x

We kwadrateren beide leden van de twee uitdrukking:

y²=2*p*x
y²=⁹/₄*p² + x² - 3*p*x

Stel nu beide rechterleden gelijk aan mekaar en dan bekom je een kwadratische vergelijking in x. De oplossingen zijn x=^p/₂ en x=⁹/₂*p (controleer zelf eens!). Merk op dat de eerste oplossing niet anders is dan de x-coordinaat van het punt Q.

We bepalen nu de vgl van de raaklijn aan de parabool in x=⁹/₂*p aan de hand van het eerder vermelde formuletje. De raaklijn wordt:

-3*y*p=p*(x+^p/₂)

of na deling door -p:

3*y=-(x+^p/₂)

SAMENVATTING

y=x+p/2
y=-p
y=-1/3*x-3/2*p

We hebben nu de vgl van alle drie de rechten. Snijden deze elkaar in één punt? Dat wil zeggen: als we deze drie vergelijkingen in een stelsel tezamen beschouwen, bestaat er precies één oplossing!!! Dit is het geval als de determinant van het stelsel = 0 (dit heb je gezien in lineaire algebra in het vijfde middelbaar).

De determinant wordt:

1 1 1/2*p
1 0 -1*p
1 1/3 3/2*p

Deze determinant is altijd nul! Verifieer zelf. Hiermee is het bewijs geleverd!!!

Groetjes
Indien er nog vragen zijn, stuurt u maar een berichtje :).

Igor

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 september 2004