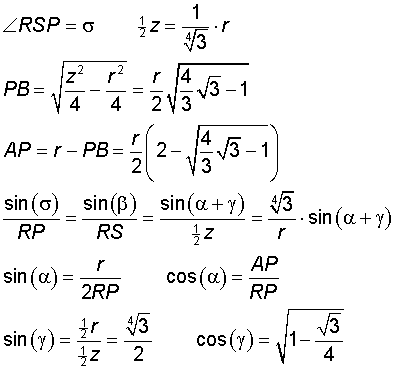WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gelijkzijdige driehoek en vierkant met dezelfde oppervlakte

Er is een spaarpot van de ABN-AMRO waar je in drie scharnierpunten (het vooraanzicht) kunt laten overgaan van een vierkant in een gelijkzijdige driehoek, en omgekeerd.
Je zou dus moeten kunnen bewijzen dat de gekozen constructie exact is.

Ik ben er al een aantal maal aan begonnen en met (analytisch) snijden van lijnen en cirkels proberen het antwoord te vinden. Ik raak verstrikt in wortels en breuken.
Weten jullie of er ergens iets over te vinden is?

Nadere toelichting:

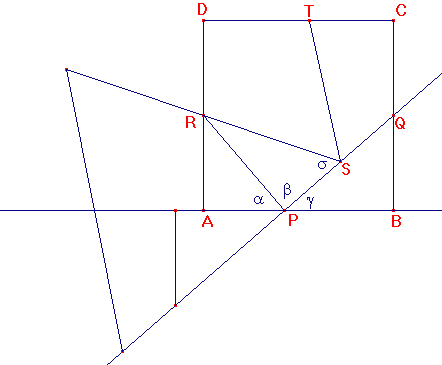
Teken vierkant ABCD
Q is het midden van BC en R is het midden van AD.
Noem de zijde van het vierkant r.
De oppervlakte van het vierkant is dan r².
Noem de zijde van de gelijkzijdige driehoek z.
De oppervlakte van de driehoek is dan ¹/₂·z·¹/₂z√3 = ¹/₄√3·z².

Uit de gelijke oppervlakte van de driehoek en het vierkant volgt dat z = 2/3^0.25·r
(dus 2 gedeeld door de vierdemachtswortel uit 3 maal r)
en ¹/₂z = 1/3^0.25·r.
Q is het midden van BC.

Cirkel vanuit Q de lengte ¹/₂z om naar AB, het punt op AB dat je krijgt noem je P.
Trek PQ.
R is het midden van AD.
Cirkel vanuit R de lengte ¹/₂z om naar PQ, het punt op PQ dat je krijgt noem je S.
S lijkt het midden van PQ, maar dat is net niet zo. Later meer daarover.

Cirkel tenslotte vanuit S de lengte ¹/₂z om op CD, het punt op CD dat je krijgt noem je T.

Als je deze constructie uitvoert en dan de 4 stukken van het vierkant uitknipt,
Dan kun je van een vierkant een gelijkzijdige driehoek maken.

Als je wilt bewijzen dat het echt klopt, dan kun je inzien dat het bewijs eigenlijk neerkomt
op het bewijzen dat $\angle$RSP = 60°.
Rob va
Docent - donderdag 2 september 2004

Antwoord

dag Rob,

In een vervolgvraag formuleerde je bovenstaande nadere toelichting, en vermeldde bovendien dat je de oplossing al gevonden had.

Omdat ik het een intrigerend vraagstuk vind, heb ik hem toch in behandeling genomen. Benieuwd of mijn oplossing overeenkomt met die van jou.

Ik heb het opgelost met de sinusregel:

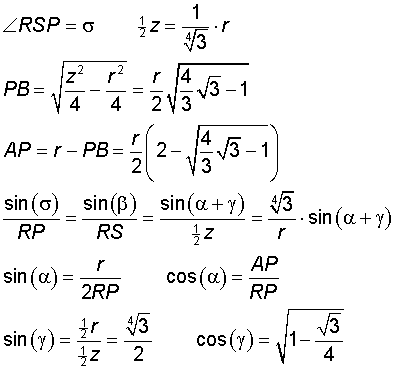
RP en r vallen uit de vergelijking weg.
Uitwerken levert uiteindelijk het antwoord: sin($\sigma$) = ¹/₂√3, waarmee het gevraagde bewezen is.
Ik houd me aanbevolen voor dergelijke vragen.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 5 september 2004