WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte bepalen van figuur begrensd door 2 functies en de x-as

Beste,

Het betreft de volgende opgave:

De oppervlakte van de kleinste vlakke figuur die begrensd wordt door de parabool f(x): y²=4x, de rechte g(x): y = 2x-4 en de x-as bedraagt........

A: 3
B: 5/2
C: 7/3
D: 4Ö(2/3)

Deze opgaven moet ik zonder rekenmachine zien te beantwoorden.
Allereerst heb ik in ieder geval de snijpunten met de x-as berekend. Waaruit volgt voor f(x) (0,0) en g(x) (2,0)
Ook het snijpunt van de grafieken zal ik (denk ik) moeten berekenen:
Ö(4x) = 2x-4 ???????
Zou u mij verder kunnen helpen met:
Het oplossen van deze vergelijking

Het primitiveren:
F(x): 2 2/3 xÖx
G(x): x²-4x

Vervolgens de ingraal opstellen van ... tot ...
hoogste grafiek - laagste grafiek, maar wat moet ik dan met die x-as doen????

Kunt u mij verder helpen met deze opgave???

Alvast ontzettend bedankt!
Groeten
Annelies
Anneli
Leerling bovenbouw havo-vwo - maandag 30 augustus 2004

Antwoord

dag Annelies,

Ik weet niet of je al een plaatje getekend hebt van de grafieken, want dat is meestal erg handig. Zeker als je moet kiezen voor de kleinste van twee vlakdelen.

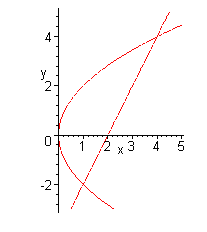
In jouw geval ligt het kleinste deel onder de x-as.
Om de snijpunten van de grafieken te berekenen, kun je beter de x substitueren dan de y, omdat je dan geen wortel hoeft te trekken.
dus:
y = ¹/₂y² - 4
Oplossen geeft: y = 4 of y = -2
Kun je de bijbehorende x-waarden berekenen?
Om nu de gewenste oppervlakte te berekenen, verdeel je dit vlakdeel in twee delen. Voor het ene deel primitiveer je f, maar dan wel de 'negatieve' poot van f, dus
y = -Ö(4x) = -2Öx
Deze primitieve is -4/3 xÖx (maar misschien bedoelde je dat ook).
Voor het tweede deel primitiveer je g (dat heb je goed gedaan), en je vult de juiste grenzen in.
Lukt dat?
succes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 30 augustus 2004