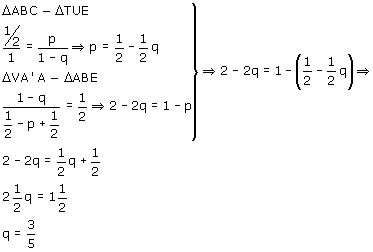WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Haga-theorie, vouwkunst en wiskunde

Deze theorie van de Japanner Kazuo Haga is oorspronkelijk ontwikkeld voor origami (Japanse vouwkunst) maar is wiskundig zeer interessant. Maar hoe lever je het bewijs? Om deze vraag te kunnen beantwoorden eerst de theorie:

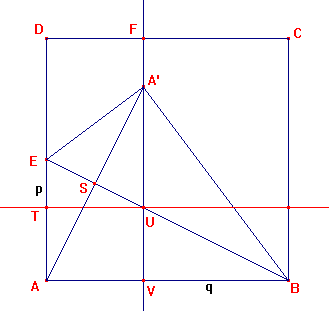
Neem een vierkant stuk papier zijde 1. Noem de hoeken ABCD (beginnend met de linker onderhoek en tegen de klok in). Markeer nu de helft van zijde AD met punt E zodat AE=AD=¹/₂

Maak nu een vouw van E naar hoekpunt B, zodat hoek A omhoog wordt gevouwen. Maak nu een vouw loodrecht op zijde CD maar door de omgevouwen hoek A. Deze vouw snijdt zijde CD in punt F. Nu is DF=2/5 en CF=3/5. De vraag is: waarom, wat is het bewijs, zonder uiterst vergaande ingewikkelde meetkunde en goniometrie...?

Deze theorie is uiterst interessant en is nog verder toe te passen tot een 7-deling van een zijde. Als je namelijk punt E verlegt zodat deze niet op de helft van AD ligt maar op 2/5 (en we hebben net gezien hoe je dat doet)dus AE=2/5 en DE=3/5. Als je dan vouwt over lijn EB en de procedure hierboven herhaalt dan kom je uit op DF=2/7 en CF=5/7...

Leuk hè? Maar het bewijs?
WA
Student universiteit - zondag 25 juli 2004

Antwoord

Met een beetje elementaire meetkunde (gelijkvormigheid) gaat het best:

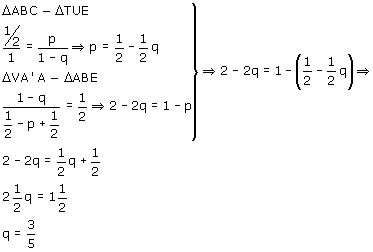
Probeer die andere zelf maar eens.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 juli 2004