WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Welke waarde van x voldoet aan de vergelijking

Goedenmiddag, ik heb hier een moeilijke vraag;

Welke van de volgende waarden van x voldoet aan de vergelijking;
2cos²(3x + 30°)= 1

Het antwoord is 155°, maar kom tot hier;
cos( 3x + 30°) = Ö0,5

weten jullie hoe het verder moet?
Bij voorbaat dank.
Bas
Leerling bovenbouw havo-vwo - dinsdag 20 juli 2004

Antwoord

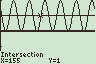Hiernaast zie je de grafiek van:
f(x)=2·cos²(3x+30) op het domein [0,360]. Op dat interval zie ik wel 12 oplossingen! En inderdaad zit x=115° er ook bij. Hoe zit dat?

Hieronder zie je een tabel met waarden voor sinus en cosinus van een aantal bekende hoeken.

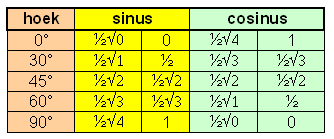
Omdat Ö(0,5)=¹/₂Ö2 kan je verder:

cos(3x + 30°) = ¹/₂Ö2
3x + 30° = 45° + k·360° of 3x + 30° = -45 + k·360°

Maar je bent wel 'iets kwijt geraakt!'. Er geldt namelijk ook:
cos(3x + 30°) = -¹/₂Ö2
Enz...

Nou jij weer..

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 20 juli 2004

Re: Welke waarde van x voldoet aan de vergelijking