WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

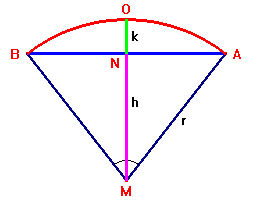
Berekening pijl van een cirkelboog

Een cirkel van 25 meter diameter verdelen in stukjes van 60 cm. De 2 uiteinden van die boog van 60cm verbinden als AB en op de helft van die lijn AB de pijl trekken naar de boog. Wat is de hoogte van die pijl?
Bestaat er een eenvoudige formule voor die berekening?
Met vriendelijke groeten,
Moscho
Ouder - zondag 18 juli 2004

Antwoord

Een formule? Ok! Zie tekening! We hebben een cirkel met een diameter d. Het cirkelboogje heeft de lengte q.

$
\begin{array}{l}
\angle AMB = \frac{q}{{\pi d}} \times 360^\circ \\
\cos \left( {\angle OMA} \right) = \frac{h}{{\frac{1}{2}d}} \\
h = \frac{1}{2}d \cdot \cos \left( {\angle OMA} \right) = \frac{1}{2}d \cdot \cos \left( {\frac{q}{{2\pi d}} \times 360^\circ } \right) \\
ON = \frac{1}{2}d - \frac{1}{2}d \cdot \cos \left( {\frac{q}{{2\pi d}} \times 360^\circ } \right) = \\
ON = \frac{1}{2}d\left( {1 - \cos \left( {\frac{q}{{2\pi d}} \times 360^\circ } \right)} \right) \\
\end{array}
$

't Is een heel gedoe, maar dan heb je ook wat! Vul je getallen maar eens in...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 19 juli 2004

Re: Berekening pijl van een cirkelboog