|
|
|
\require{AMSmath}



Betrouwbaarheidsinterval voor percentages
Geachte heer/mevrouw,
Ik heb een klein onderzoek gehouden over de naamsbekendheid van een volleybalclub. Ik heb hiertoe een enquete gemaakt met vragen waarop studenten met ja of nee konden antwoorden. Op dit moment heb ik bij alle vragen ja en nee percentages. Op de vraag of de respondenten de club kennen, heeft bijvoorbeeld 23 % nee en 77 % ja geantwoord. Ik wil graag 95 % betrouwbaarheidsintervallen voor deze percentages maken. Ik heb hiervoor een binomiale formule gebruikt omdat ik ja/nee antwoorden heb die per persoon onafhankelijk van elkaar zijn. In mijn statistiekboek stond dat ik betrouwbaarheidsintervallen kan maken voor p met de formule p = p^ +/- z($a/2)* Í[(p^*(p^-1)/n)]. Bij kleine percentages is dit echter een probleem omdat het interval in dit geval negatieve waarden bevat. Ik zou graag willen weten of ik wel de juiste formule gebruik. Mijn n is soms 80 en soms 160. Ook zou ik willen weten of ik het niet met een binomcdf plot kan doen. Ik teken dan de binomcdf in mijn grafische rekenmachine samen met een 0,025 en 9.975 lijn. De snijpunten neem ik als grenspunten voor het interval. De uitkomsten van deze methode komen niet precies overeen met de formule-methoden (vooral niet bij kleine waarden), dus ik denk dat het niet kan. Maar als dit niet kan, zou ik graag willen weten waarom het niet kan.
Alvast bedankt!
Martin
Student universiteit - woensdag 14 juli 2004
Antwoord
De formule die je moet gebruiken is:
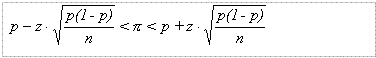
In deze formule is de z waarde 1,96 p=0,77
Nu mag deze formule gebruikt worden indien nĚp 5 en nĚ(1-p) 5 en nĚ(1-p) 5. Bij n=80 gaat dit dus mis bij percentages die onder de 6% of boven de 94% liggen. Dat komt omdat je dan eigenlijk niet met een normale benadering mag werken. 5. Bij n=80 gaat dit dus mis bij percentages die onder de 6% of boven de 94% liggen. Dat komt omdat je dan eigenlijk niet met een normale benadering mag werken.
Wanneer wel aan de bovenstaande eisen voldaan is dan krijg je ook zeker geen uitkomsten onder de 0% of boven de 100%.
De formule is dus juist indien je aan de genoemde eisen voldoet.
Dat je met een rekenmachine een iets andere uitkomst uitkrijgt kan liggen aan het feit dat je rekenmachine de binominale verdeling niet benadert en omdat je bij bovenstaande formule zelf geen continuiteitscorrectie toepast.
Met vriendelijke groet
JaDeX

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 juli 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








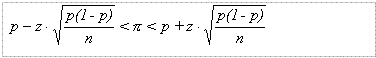
 5 en nĚ(1-p)
5 en nĚ(1-p)
