WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verwachtingswaarde van het aantal te spelen sets bij tennis

Twee tennissters A en B spelen vaker tegen elkaar en gemiddeld wint A 60% van de sets. De speelsters ontmoeten elkaar op een toernooi in een best-of-five match (dus
wie het eerst drie sets wint heeft gewonnen).

ii. Bereken de verwachtingswaarde voor het aantal sets die de match duurt.

Ik wil alleen weten hoe ik het tweede deel aanpak. Ik dacht dat ik de kans dat A won kon vermenigvuldigen met de kans dat B won en het variabele aantal sets. Dan zou ik dat gelijk stellen aan de match (0.6 · 0.4 · N = 5), maar dan komt uit dat de verwachte aantal sets 20.833 is. Dit kan dus nooit waar zijn, denk ik

Bij voorbaat dank.
BZ
Student universiteit - dinsdag 6 juli 2004

Antwoord

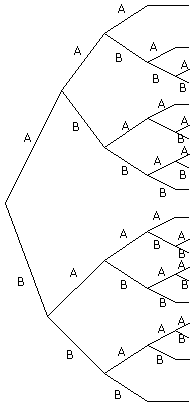Teken eerst een boomdiagram!

Er zijn 2 manieren waarop de partij in 3 sets afgelopen kan zijn. AAA of BBB
P(AAA)=0,6³ en P(BBB)=0,4³
P(in 3 sets)=...

Er zijn 6 manieren waarop de partij in 4 sets gespeeld kan worden....
Daarbij kan A winnen of B kan winnen....

A wint: AABA, ABAA, BAAA
P(A wint in 4 sets)=3·0,6³·0,4
P(B wint in 4 sets)=3·0,6·0,4³

Doe hetzelfde voor 'B wint in 4 sets'. De kans op 4 sets is dan weer de som van P(A wint in 4 sets) en P(B wint in 4 sets)

Tenslotte is de kans dat de partij 5 sets duurt 1-P(3 of 4 sets).

Om de verwachtingswaarde uit te rekenen van het aantal sets vermenigvuldig je steeds de kans 'n sets' met 'n'.

E(sest)=P(3 sets)·3 + P(4 sets)·4 + P(5 sets)·5

En dan ben je er...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 7 juli 2004