|
|
|
\require{AMSmath}
Kubussen stapelen
Men stapelt kubussen opeen. De eerste kubus heeft een ribbe van 1 m de tweede van 1/2 m, de derde een van 1/3 m enz.
Bestaat er een gebouw waarin men deze kubussen zou kunnen opstellen? Kan men een beperkte hoeveelheid verf kopen om deze kubussen te schilderen?
patric
3de graad ASO - woensdag 9 juni 2004
Antwoord
Vraag 1 komt neer op de de vraag of de som 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 ....... eindig is. Dat is dus niet het geval.
Als volgt kun je dat zien: in de onderstaande figuur is de som van de bovenstaande reeks terug te vinden als de totale oppervlakte Opp van de getekende rechthoeken.
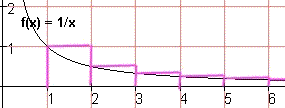
Uit de tekening blijkt dat Opp  1ò¥ 1/x dx = ln x 1]¥ en dit wordt dus zelf oneindig groot. Hiermee is aangetoond dat de oorspronkelijke reeks onbegrensd is.
De totale oppervlakte van de kubussen is 6 keer 1/12 + 1/22 + 1/32 + 1/42 + ....
De vraag is nu of deze som wel eindig is. En dat is hij inderdaad want:
1/12+1/22+1/32+1/42+ .....  1+ 1/(1·2) + 1/(2·3) + 1/(3·4) + ..... =
1+ 1-1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ...... 2
Dus is de totale oppervlakte kleiner dan 6x2=12
Deze laatste kan overigens ook met een integraal worden afgeschat, uiteraard mag je dat nu zelf proberen.
Toch een erg aardige manier om dit probleem te verpakken 
Met vriendelijke groet
JaDeX
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 9 juni 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
