WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Projectie cirkel op een rechte

Ik bekijk een cirkel (schijf) zijwaarts vanuit een camera.
Op het camerabeeld krijg ik een lijn met X aantal pixels.
X komt overeen met de diameter D van de cirkel.
Elke pixel P heeft een vaste grootte en komt overeen met een bepaalde booglengte B.
Is het mogelijk een formule te schrijven die mij B geeft in functie van P?

Rudi
Iets anders - dinsdag 8 juni 2004

Antwoord

dag Rudi,

Ik neem aan dat je bedoelt:
p is het rangnummer van de pixel op het lijnstuk.
Geef een functie van de lengte van het boogje dat geprojecteerd wordt op de pixel nummer p.
X is het aantal pixels.
Ik neem voor het gemak even aan dat X even is.
Het is handig om p te laten lopen van ^(-X)/₂ tot ^(X)/₂-1
Dus bijvoorbeeld als X=6, dan is p achterenvolgens -3, -2, -1, 0, 1 en 2).
p=0 correspondeert met de pixel die begint in het midden.
De lengte-eenheid is steeds de pixel.
Ik geef alleen de formule voor p0.
Noem de straal van de cirkel r (dus r=^X/₂)

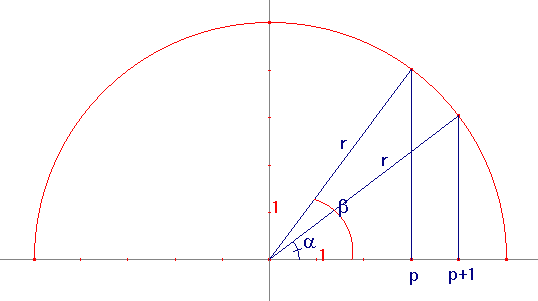
Er geldt:
cos(a) = ^p+1/_r, dus a = arccos(^p+1/_r)
Ook:
cos(b) = ^p/_r, dus b = arccos(^p/_r)
Hiermee heb je een uitdrukking voor de tussenliggende hoek:
b-a = arccos(^p/_r)-arccos(^p+1/_r)
Deze hoek vermenigvuldigen met de straal r levert de gevraagde booglengte B in pixels.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 juni 2004