WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Grootste volume van kegel uit cirkelsector

Hallo ... ik wou even vragen of jullie me een (uitgewerkt) voorbeeld kunnen laten zien van een extremumvraagstuk over een CIRKELSEGMENT.

EN graag had ik dan ook meer uitleg gewild bij het volgende vraagstuk.

Uit een cirkelvormige blad papier met straal R snijden we een sector uit met middelpuntshoek a. Met deze sector maken we een kegel. Hoe groot moeten we a nemen opdat het volume van de kegel zo groot mogelijk zou zijn.

Hopelijk kunnen jullie me helpen want vrijdag heb ik examen.

ALVAST BEDANKT !!!
Cihan
3de graad ASO - maandag 7 juni 2004

Antwoord

dag Cihan,

Hier alvast een antwoord op je tweede vraag.

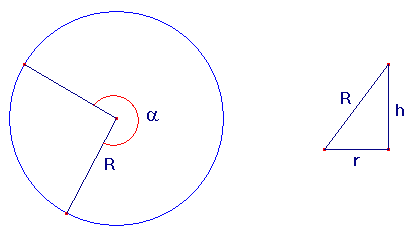
Neem a in radialen.
Dan is de lengte van de boog van de sector gelijk aan a·R
Dit wordt de omtrek van het grondvlak van de kegel.
Hieruit kun je de straal r van dit grondvlak berekenen:
r = a·R/(2p)
De oppervlakte van het grondvlak is dan p·r²
De hoogte van de kegel is h, die te berekenen is met de stelling van Pythagoras (zie het driehoekje in de tekening).
Wetende dat het volume van de kegel gelijk is aan
¹/₃·(opp grondvlak)·hoogte
heb je hierbij een uitdrukking voor dit volume.
Differentiëren naar a en deze afgeleide gelijkstellen aan 0 levert de kandidaten op voor de waarde van a met het maximale volume.
Lukt dat verder?
succes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 juni 2004

Re: Grootste volume van kegel uit cirkelsector