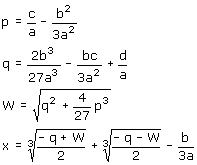WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formule van Cardano

ik heb een vergelijking die ik maar niet kan oplossen met de formule van Cardano
Maar ik had ook ergens gelezen dat je door middel van complexe getallen toch de x'en kan berekenen.
( als ik deze vergelijking invoer in de grafische rekenmachine krijg ik drie uitkomsten )
de vergelijking is : 2x³+6x²-20x-48=0
en mijn vraag is hoe bereken je de x'en van deze vergelijking en kan je de formule van Cardano gebruiken ( als dat kan wil ook zien hoe u dat doet )
Sebaha
Leerling bovenbouw havo-vwo - donderdag 13 mei 2004

Antwoord

Hallo Sebahat,

De vergelijking 2x³ + 6x² -20x - 48 =0 geeft na de nodige tussenstappen
de vergelijking g² - 12g + 2197/27 = 0
De discriminant van deze vergelijking is - 4900/27.

De vergelijking heeft dus geen oplossingen in .
In (met complexe getallen) is deze vergelijking wel op te lossen.

Als je heel dapper bent kun je met een van de oplossingen verder rekenen om één oplossing van de vergelijking te berekenen.Daarna kun je met behulp van de factorstelling de andere waarden berekenen.

Wanneer je de GRM instelt op complexe getalllen (MODE a + bi) dan kun je met de volgende
formule x berekenen.

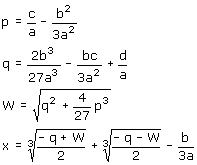
p = -13
q = -12
w = 9,670238545i
x = 3

Een van de oplossingen is dus x = 3. Door gebruik te maken van de factorstelling krijg je de
oplossingen x = -2 en x = -4

Zie Welke formule is nu precies de formule van Cardano?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 13 mei 2004