|
|
|
\require{AMSmath}
Eindexamen 2002-1 opgave 9
Op www.havovwo.nl kwam ik de vraag ëen beweging door (0,0) tegen.
x(t)= cos(15t) + cos(2t)
y(t)= sin(15t) + sin(2t)
In vraag 9 wordt gevraagd om te bewijzen dat dit stelsel gelijk is aan
x(t) = r(t)*cos(8,5t)
x(t) = r(t)*sin(8,5t)
met r(t) = 2cos(6,5t)
Op dezelfde site is een 'tussenantwoord' gegeven, waar ik niet veel verder mee kom.
Als ik stel dat a = 7,5t en b = t moet dus worden bewezen dat
1. cos(2a) + cos(2b) = 2cos(a+b)cos(a-b)
2. sin(2a) + sin(2b) = 2sin(a+b)sin(a-b)
Wanneer ik beide gevallen uitwerk met de regels voor sin(t+u) en cos(t+u) loop ik vast bij de vergelijking
1A. cos(2a) + cos(2b) = 2sin(a)cos(a) + 2sin(b)cos(b)
1B. 2cos(a+b)cos(a-b) = 2cos^2(a)cos^2(b)- 2sin^2(a)sin^2(b)
2A. sin(2a) + sin(2b) = 2sin(a)cos(a) + 2sin(b)cos(b)
2B. 2sin(a+b)sin(a-b) = 2sin^2(a)cos^2(b)- 2sin^2(b)cos^2(a)
want hier moet dus gelden
2sin(a)cos(a)+2sin(b)cos(b) = 2cos^2(a)cos^2(b)-2sin^2(a)sin^2(b), en
2sin(a)cos(a)+2sin(b)cos(b) = 2sin^2(a)cos^2(b)- 2sin^2(b)cos^2(a), ofwel
sin(a)cos(a)+sin(b)cos(b)= sin^2(a)cos^2(b)-sin^2(b)cos^2(a)
Wat zie ik over het hoofd?/ Waarom kom ik hier niet verder?
Thijs
Student hbo - woensdag 5 mei 2004
Antwoord
Hallo Thijs,
Pas op (1) en (2) eens de volgende formules van de formulekaart toe:
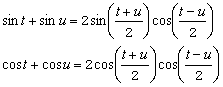
wl
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 6 mei 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
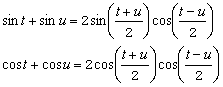
Re: Eindexamen 2002-1 opgave 9