|
|
|
\require{AMSmath}



Combinatie of permutatie?
Een vraagje,
Bij combinaties is de volgorde niet belangrijk, dus dit zou moeten betekenen dat je maar 1 combinatie hebt als je weet dat je 7 termen hebt (3x S en 4x M). Want bijvoorbeeld MMMMSSS =MSMSMSM, als je puur en alleen kijkt naar combinaties.
In mijn boek staat echter de volgende vraag.
c)hoeveel series heb je met 3x S en 4x M. Het antwoord moet 35 zijn en dit vind ik erg vreemd want hieraan kun je slechts komen door er vanuit uit te gaan dat je toch via combinaties moet rekenen zodat dan 7 boven 3 het antwoord geeft. Ik dacht namelijk dat je maar 1 combinatie hebt en toch kun je het antwoord via de 'combinatiemanier' krijgen! Aangezien de volgorde bij de vraag wel uitmaakt (gezien het antwoord o.a.) ging ik er vanuit dat ik met permutaties zou moeten werken, want hierbij wordt dus juist wel op de rangschikking (waarover het allemaal gaat) gelet. Waar zit de denkfout, ja, dat is de vraag.
Alvast bedankt voor het antwoord,
JOp
Jop No
Leerling bovenbouw havo-vwo - donderdag 22 april 2004
Antwoord
Hallo Jop,
Je hebt 7 plaatsen voor 4 keer de letter M.
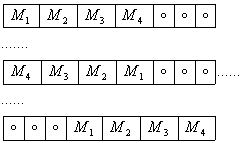
Als we voor het aantal rijtjes permutaties gebruiken dan wordt het aantal =7.6.5.4=840.
Maar de letters M hebben geen nummer en zijn dus onderling uitwisselbaar. Het aantal rijtjes wordt dus
840/4! =35.Dit is het zelfde als (7 boven 4).
We hebben nu per rijtje 3 plaatsen voor 3 keer de letter S.
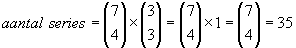
Werk je met 4R,3B en 2W dan krijg je:
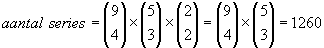
wl
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 22 april 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|









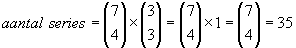
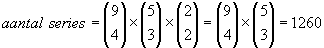

 Re: Combinatie of permutatie?
Re: Combinatie of permutatie?