|
|
|
\require{AMSmath}



Hilbert-matrix
In onze cursus wordt de Hilbert-matrix gedefinieerd als
Hn:=
[ [ 1 1/2 1/3 ... 1/n ]
[ 1/2 1/3 1/4 ... 1/(n+1) ]
...
[ 1/n 1/(n+1) .... 1/(2n-1) ]]
Daarop wordt een recursieve formule voor de determinant gepropositioneerd als volgt:
(n-1)^2*(n-2)^2*...*2^2*1
det(Hn)= ------------------------- * det(H(n-1))
n^2*(n+1)^2* ... *(2n-2)^2*(2n-1)
Ik vraag me af hoe je dit moet bewijzen. Ik heb al veel geprobeerd maar 't wil me maar niet lukken.
Dank bij voorbaat
Jan
Student universiteit - woensdag 21 april 2004
Antwoord
Beste Jan,
Geen gemakkelijke opgave. De manier om dit probleem aan te pakken is in dit geval, door het te veralgemeniseren. We bekijken de matrix
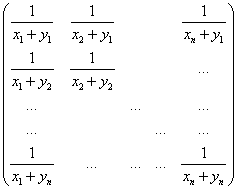
Natuurlijk vinden we voor xi=1 t/m n en yj=0 t/m n-1 precies de Hilbert matrix.
Gaan we nu van deze algemenere matrix de determinant bepalen, dan weten we dat dat een uitdrukking wordt van graad -n.
Door gelijknamigmaken zien we dat de noemer van de determinant moet worden Õ(xi+yj). De graad van de noemer is dus n2.
Als je de eerste kolom vermindert met de tweede kolom blijft de determinant gelijk. Maar je ziet wel dat in de eerste kolom uitdrukkingen komen van de vorm:
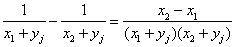
waaruit blijkt dat (x1-x2) een deler is van de teller van de determinant, want het deelt alle elementen van de eerste kolom.
Met een soortgelijke redenering, maar dan met de eerste twee rijen, zien we dat (y1-y2) een deler is van de teller van de determinant.
Maar we kunnen ook andere paren kolommen of rijen nemen. Hieruit leiden we af dat de teller kennelijk deelbaar is door Õ(xi-xj)(yi-yj) waarbij het product loopt over paren 1 i i j j n. n.
De teller heeft dus een graad van n2-n
Combineren we teller en noemer dan zien we dat de graad van de teller en noemer, dan vinden we graad -n. We zijn er dus op een constante na. Deze constante is 1. Dat kun je inzien door afschattingen te maken wanneer je xi en yj hard laat groeien. Uit de afschattingen haal je de constante.
Zo hebben we een directe formule voor de determinant van Hn.
Jouw recursieve formule zal ook vrij eenvoudig volgen.
Zie Hilbert matrix

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 11 mei 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








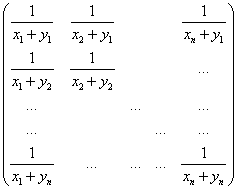
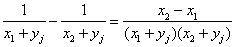
 i
i j
j
