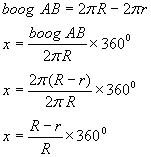WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Inhoud van de kegel

Mijn vraag is hoe je de overlappingshoek van een cirkel schijf van een kegel kunt berekenen?
En nog een andere vraag is, de formule van een kegel is 1/3·p·r²·h , maar hoe kun je de formule van de inhoud van een kegel uitgedrukt in alleen de straal r van de grondcirkel formuleren?

Al vast bedankt
met vriendelijke groeten enny
Enny
Leerling bovenbouw havo-vwo - donderdag 15 april 2004

Antwoord

Hallo Enny,

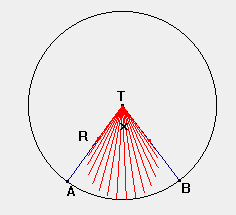
R is de straal van de cirkel waarvan we de kegelmantel maken.
r is de straal van de grondcirkel.
x is de overlappingshoek.

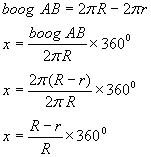
Hoofdletter R en kleine letter r moeten wel bekend zijn.(anders is je vraag niet te beantwoorden)

Met een beetje knip en plakwerk kunnen we de volgende kegel maken.

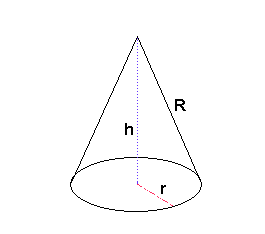
Met behulp van de stelling van Pythagoras kun je h uitdrukken in R en r.
We krijgen dan de volgende formule voor de inhoud van de kegel:

I = ¹/₃pr²Ö(R²-r²)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 15 april 2004