WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Het 3 tegen 1 probleem

hoi iedereen

tijdens de les heb ik de opdracht gekregen om het 3 tegen 1 probleem op te lossen.

dat houd in: in een dobbelspel heeft spelerA 3 dobbelstenen en speler B heeft er 1. speler A wint alleen wanneer zijn hoogste aantal ogen hoger is dan het aantal ogen van speler B, speler B wint dus wanneer zijn aantal ogen gelijk of hoger is dan het aantal ogen van speler A.
Dan is de vraag: hoe vaak wint speler A en hoe vaak wint speler B?

hoe bereken je dit?

alvast bedankt
groetjes Britt
britt
Leerling onderbouw vmbo-havo-vwo - donderdag 8 april 2004

Antwoord

Een heel aardig opgaafje waarvan de oplossing verbluffend eenvoudig kan zijn als je ziet hoe het moet.
Goed..... dat lukt dus wel met enig denkwerk en rekenwerk.
Van belang om in te zien wat de kansverdeling wordt van de score van speler A. Wanneer speler A met twee dobbelstenen zou gooien is dat nog wel te tekenen, dat ziet er dan als volgt uit.

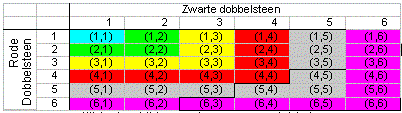
Het aantal vakjes met hoogste score 4 is hierbij 7. (de rode vakjes !!). Niet dit aantal is interessant maar het patroon dat ontstaat.
Het aantal vakjes met score 4 is namelijk 4²-3², het aantal vakjes met score 6 is 6²-5² enzovoort.
Probeer nu voor je zelf voor te stellen wat er bij drie dobbelstenen gebeurt. Dat kun je voorstellen als een drie-dimensionale 6x6x6 kubus. Een maximale score van 1 krijg je alleen bij (1,1,1). Dus 1 blokje. Een maximale score van 2 krijg je dan bij 2³-1³=7 blokjes. Max score 3 bij 3³-2³=19 blokjes enzovoort. Dat levert de kansverdeling op van het maximale aantal ogen van 3 dobbelstenen.

Nu nog kijken wanneer je met 3 dobbelstenen gaat winnen, de blauwe vakjes in de volgende figuur geven dat aan.

Met de kansverdelingen in tabel 2 kun je nu ook de kans op winst voor A berekenen.
(hoogste waarde 2): 7/216·1/6
(hoogste waarde 3): 19/216·2/6
(hoogste waarde 4): 37/216·3/6
(hoogste waarde 5): 61/216·4/6
(hoogste waarde 6): 91/216·5/6
Deze waarden uitrekenen en allemaal optellen: is ongeveer 66%.
Voor de onderbouw toch best pittig. Duidelijk genoeg ??

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 9 april 2004

Re: Het 3 tegen 1 probleem