|
|
|
\require{AMSmath}



Telprobleem vriendenkring en werknemers
Ik zit al een hele tijd te knoeien met 2 vragen, bij de eerste staat er op WisFaq een soortgelijke vraag, maar dat helpt met niet goed, want ik heb het steeds verkeerd..
1)
Tot een vriendenkring van een gezin behoren 17 personen. Op hoeveel manieren kan dit gezin 8 onder hen op een feestje uitnodigen als 2 onder deze vrienden niet op elkaar gesteld zijn en niet samen wensen aanwezig te zijn?
Ik heb het totaal uitgerekend en ik kom dan op 17 boven 8 = 24310, dan heb ik gerekend als die vrienden samen zouden komen = (15 boven 8) + (16 boven 6) = 11440 en dan heb ik 24310-11440 gedaan kwam ik uit 12870 maar dat blijkt niet te kloppen.. wat heb ik fout gedaan?
2)
De tweede vraag begrijp ik niet hoe ik dat moet uitrekenen: Op hoeveel manieren kan men 9 opdrachten verdelen onder 26 werknemers, als 5 ervan slechts kunnen uitgevoerd worden door 15 van de 26? Merk op: elke werknemer kan maar 1 taak uitvoeren
ik hoop dat u me kunt helpen, alvast bedankt
Promis
Iets anders - woensdag 7 april 2004
Antwoord
Antwoord op vraag 1)
Je kunt dit vraagstuk op twee manieren te lijf gaan. Jouw manier; totaal aantal mogelijkheden - aantal mogelijkheden als ze beide mee gaan. Of je kunt twee aparte situaties bekijken:
Situatie I: Geen van beide gaat mee
Situatie II: Eén van de twee gaat mee (2x)
Bij jouw manier maak je een fout met het aantal mogelijkheden wanneer beide mee gaan, want dat is 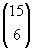 . Toelichting: ze gaan beide mee en dan moet je nog het aantal mogelijkheden van 6 personen uit de 15 overige bekijken. . Toelichting: ze gaan beide mee en dan moet je nog het aantal mogelijkheden van 6 personen uit de 15 overige bekijken.
Doe de andere manier zelf, daar komt het zelfde uit als je het goed hebt gedaan.
Antwoord op vraag 2)
Verdeel eerst de 5 'speciale' opdrachten onder de 15 'specialisten'. Op hoevel manieren kan dat? Op hoeveel manieren kan je dan de rest van de opdrachten verdelen over de overige 21 werknemers (inclusief de 10 overige specialisten)? En moet je die uitkomsten dan vermenigvuldigen of optellen? Als je hier eens over nadenkt moet het lukken.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 8 april 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








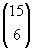 . Toelichting: ze gaan beide mee en dan moet je nog het aantal mogelijkheden van 6 personen uit de 15 overige bekijken.
. Toelichting: ze gaan beide mee en dan moet je nog het aantal mogelijkheden van 6 personen uit de 15 overige bekijken.
