WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hulp bij een bewijs van de stelling van Pythagoras

hoi
Ik moet voor school een werkstuk maken over de stelling van Pythagoras.
Nu had ik een boekje waar een bewijs in stond. maar ik snap het bewijs niet dus kan een van jullie me helpen met wat ze hiet mee bedoelen?
Dit plaatje hoort erbij:

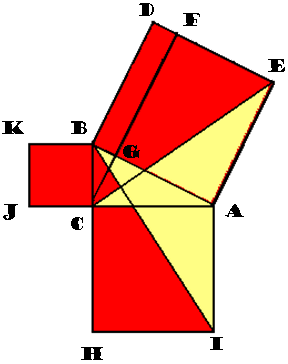
...en ik heb al bewezen dat de driehoek ABC AGC en CBG gelijk zijn en nu staat er bij hun als conclusie:
BC gelijk aan BG als AB gelijk is aan BC als AC gelijk is aan AG als AB gelijk is aan AC.
Dus:
A:G = C:A = A² = CG(1)
En B: (C-G) = C:B = B² = C² - CG

en hier snap ik helemaal niks van!!!
help me AUB!
alvast bedankt
renee
renee
Leerling bovenbouw havo-vwo - zaterdag 27 maart 2004

Antwoord

Beste Renee,

Je bedoelt waarschijnlijk dat je bebt laten zien dat ABC, ACG en CBG gelijkvormig zijn. Dat betekent dat de zijden van ABC vergrotingen zijn met dezelfde factor van de overeenkomende zijden van ACG en CBG. In het bijzonder betekent het ook dat de verhoudingen van de zijden van de driehoek gelijk zijn. Dus als in driehoek ABC de schuine rechthoekzijde x keer zo groot is als de grote rechthoekzijde, dan is dat in CBG en ACG ook zo.

Oftewel: BC:BG = AB:BC = AC:AG. Je kunt dit ook als delingen schrijven ^BC/_BG = ^AB/_BC = ^AC/_AG.

De fout die je nu in het verhaal hierboven gaat maken is dat je niet zomaar B mag wegstrepen uit ^BC/_BG. Het zijn niet losse variabelen B en C in de teller, maar de lengte van het lijnstuk BC. Iets heel anders dus.

Misschien dat je het bewijs nu beter kan lezen. Zo niet, dan horen we het wel.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 27 maart 2004

Re: Hulp bij een bewijs van de stelling van pythagoras