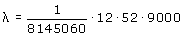WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Pincodes, lotto en de Poissonverdeling

Hoi! Ik zou graag een paar vragen beantwoord willen hebben over poisson.

1.
In een bepaalde streek vallen per maand door verlies of diefstal 700 pinpasjes in handen van kwaadwillende personen. Een onbevoegd iemand kan op dezelfde dag tot 3 keer toe een pincode proberen, bij de derde foutieve poging wordt het pasje door het pinapparaat ingeslikt. Wat is de kans dat in een gegeven maand de bankrekening geplunderd wordt van één of meer personen wiens pasjes in handen van kwaadwillende personen gevallen zijn? (Bij de beantwoording van deze vraag veronderstel dat elke kwaadwillende tot drie keer toe een pincode probeert alvorens diezelfde dag het pasje door de bank wordt geblokkeerd).

2.
In de nederlandse lotto 6/45 worden zes getallen getrokken uit 1,...,45, waarbij het totale aantal mogelijke trekkingsmogelijkheden gelijk is aan (45 boven 6)= 8145060.
Reken na dat je meer dan 9000 jaar van leven zou moeten hebben om met een kans van tenminste 50% ooit in je leven een keer de jackpot te winnen in de lotto 6/45 als je elke week 12 rijtjes zou invullen.

helluupppp!!!!
Inge
Leerling bovenbouw havo-vwo - woensdag 24 maart 2004

Antwoord

Eerst maar eens Ernstige verkeersongelukken, bijeenkomsten en de Poissonverdeling bekijken. Zie voor een samenvatting en voorbeelden de link die er bij staat.

1.
Bereken eerst het gemiddeld aantal goed te raden pincodes als je 700 keer probeert binnen 3 keer zo'n pincode te raden. Dat is je $\lambda$.
Bereken vervolgens de kans P(k$>$0)

2.
Ook hier is het de kunst om $\lambda$ te bepalen. Als je elke week 12 rijtjes invult, en dat 9000 jaar volhoudt, dan is het gemiddeld aantal keren dat je wint gelijk aan:

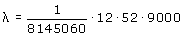
Laat zien dat P(k$>$0)$\approx$0,5

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 maart 2004