|
|
|
\require{AMSmath}



Vectoren
Hoi Wisfaq!!!
Ik zit vast bij de volgende opgave, zouden jullie me kunnen helpen?
In het parallellepipedum met bovenvlak a'b'c'd' en grondvlak abcd, stellen we e en f de snijpunten van de vlakken a'bd en b'cd' met de diagonaal [ac']
a. Bewijs: (a,e) is equipolent met (e,f) is equipolent met(f,c')
b. Leid eruit af: de vector ac' = 3 maal de vector ae
Alvast bedankt!
Groetjes
Rob
3de graad ASO - dinsdag 23 maart 2004
Antwoord
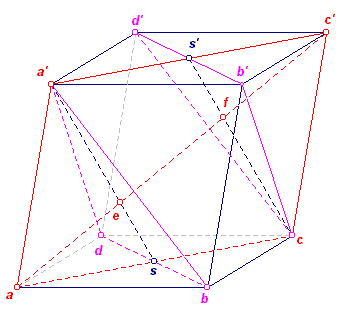
(a,e) equipollent met (e,f) equipollent met (f,c') houdt in, dat
|ae| = |ef| = |fc'|
De snijpunten e en f van ac' met de vlakken a'bd eb b'cd' liggen op de snijlijnen a's en cs' van het vlak acc'a' met die vlakken.
Nu is:
ac // a'c'
zodat
|as| : |a'c'| = 1 : 2
immers |ac| = |a'c'| en |as| = 1/2 |ac|.
Dus geldt ook:
|ae| : |ec'| = 1 : 2
waaruit direct volgt dat |ae| = 1/3 |ac'|.
Wil je direct bewijzen, dat |ae| = |ef| = |fc'|, kijk dan eens naar de driehoeken acf en a'c'e.
Hierin zijn es en fs' middenparallellen.
Ik hoop dat het bovenstaande je 'los maakt'...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 26 maart 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










