|
|
|
\require{AMSmath}



Minimaliseren
stel; we hebben drie dorpjes die besluiten om een gemeenschappelijk vliegveld te beginnen. De dorpjes liggen in een vlak elk met een x en y coordinaat. ze besluiten het vliegveld te bouwen op het punt waar de som van de kwadraten van de afstand tussen de dorpen en het vliegveld minimaal is. de vraag is; bepaal de locatie van het vliegveld.
volgens mij krijg je de volgende vergelijking voor de som van de kwadraten;
(xa-xv)2+(ya-yv)2 + (xb-xv)2+(yb-yv)2 + (xc-xv)2+(yc-yv)2
xa en ya zijn de x en y coordinaat van het punt a en xv en yv de coordinaat van het vliegveld. in principe toepassing van pythagoras.
echter hier zit ik vast; hoe valt het minimum te bepalen van deze functie en hoe kom ik achter de locatie van het vliegveld? (misschien dat gebruik van vectoren een oplossing biedt?)
bvd voor reactie
stefan
Leerling bovenbouw havo-vwo - maandag 22 maart 2004
Antwoord
Dag Stefan,
Je uitdrukking klopt, alleen noemen we zoiets geen vergelijking. Er komt ook geen =teken in voor.
Je kunt deze uitdrukking opvatten als een functie van twee variabelen, namelijk xv en yv. Voor het gemak noem ik ze maar even x en y.
Dus:
F(x,y) = (xa-x)2+(ya-y)2+(xb-x)2+(yb-y)2+(xc-x)2+(yc-y)2
Misschien ken je het principe van partiŽle afgeleide.
Daarmee kun je de uiterste waarden van een functie van meer variabelen lokaliseren. Waar de functie een minimum heeft, zijn de partiŽle afgeleiden gelijk aan 0.
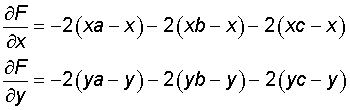
Nulstellen geeft de oplossing voor x en y, en dus voor de positie van het vliegveld.
Het grappige in dit geval is, dat het gezochte punt een bijzonder punt van de driehoek is. Het is het leukste, als je dat zelf ontdekt, dus ik zou zeggen: puzzel er nog even op. Als je er niet uitkomt, wil ik je wel verder helpen.
succes!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 22 maart 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|