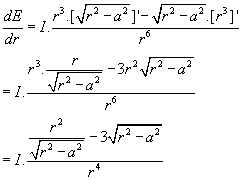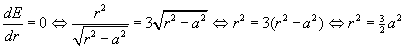|
|
|
\require{AMSmath}



Hoogte lantaarnpaal
Hallo, ik heb moet enkele opdrachten voor wiskunde maken, maar de volgende opdracht lukt me niet helemaal.
De verlichting van een weggedeelte moet worden gerealiseerd met lichtmasten langs de weg. Als een lamp daarin een lichtsterkte van Ib candťla heeft, dan is de verlichtingssterkte E (in lux) op het wegdek op een afstand van r meter van de lamp en onder een hoek a gelijk aan:
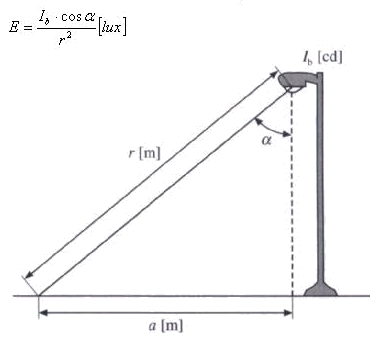
Op welke hoogte levert de lamp de hoogste verlichtingssterkte op het wegdek op een willekeurige afstand van a meter van de mastvoet?
Ik heb al geprobeerd om r uit te drukken in a, dan hou je een formule over die luidt:
E=(I*(cos(a)3)) / (h2)
(h=hoogte lantaarnpaal)
Als ik nu aanneem dat I en a constante waarden zijn dan moet ik deze formule kunnen differentieren. Als ik deze afgeleide dan aan nul gelijkstel heb ik het antwoord, ten minste dat denk ik.
Ik heb het probleem dat ik geen ster ben in differentieren en doe ik het op deze manier eigenlijk wel goed??
Rolf B
Student hbo - zondag 21 maart 2004
Antwoord
Ik zou dit denken:
de hoogte h en cosa zijn aan elkaar gerelateerd volgens:
cosa=h/r
tevens geldt dat h=÷(r2-a2)
Dus: cosa=h/r= {÷(r2-a2)}/r zodat
E = I.cosa/r2 = I.{÷(r2-a2)}/r3
differentiŽren m.b.v. de quotiŽntregel levert:
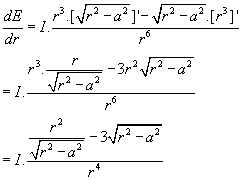
maximum waar dE/dr = 0:
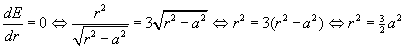
dus h=÷(3/2.a2-a2) = ÷(1/2a2) = 1/2÷2.a
groeten,
martijn
mg
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 maart 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|